题目内容
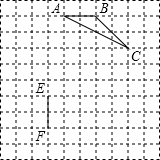 (2012•河池)如图,在10×10的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的顶点上.
(2012•河池)如图,在10×10的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的顶点上.(1)填空:tanA=
| 1 |
| 2 |
| 1 |
| 2 |
2
| 5 |
2
(结果保留根号);| 5 |
(2)请你在图中找出一点D(仅一个点即可),连接DE、DF,使以D、E、F为顶点的三角形与△ABC全等,并加以证明.
分析:(1)延长AB,过C作延长线的垂线CG,在直角三角形ACG中,由CG及AG的长,利用锐角三角函数定义求出tanA的值,利用勾股定理求出AC的值即可;
(2)图中找出一点D,连接DE、DF,△ABC≌△EFD,如图所示,理由为:在直角三角形FDM中,由FM与MD的长,利用勾股定理求出FD的长,同理求出BC的长,可得出FD=BC,同理可得出ED=AC,EF=AB,利用SSS可得出△ABC≌△EFD.
(2)图中找出一点D,连接DE、DF,△ABC≌△EFD,如图所示,理由为:在直角三角形FDM中,由FM与MD的长,利用勾股定理求出FD的长,同理求出BC的长,可得出FD=BC,同理可得出ED=AC,EF=AB,利用SSS可得出△ABC≌△EFD.
解答: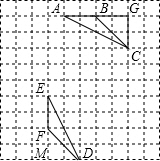 解:(1)延长AB,过C作CG⊥AB,交延长线于点G,
解:(1)延长AB,过C作CG⊥AB,交延长线于点G,
在Rt△ACG中,CG=2,AG=4,
根据勾股定理得:AC=
=2
,
tanA=
=
;
(2)图中找出一点D,连接DE、DF,△ABC≌△EFD,如右图所示,
证明:在Rt△EMD中,EM=4,MD=2,
根据勾股定理得:ED=
=2
,
在Rt△FDM中,FM=2,MD=2,
根据勾股定理得:FD=
=2
,
同理在Rt△BCG中,根据勾股定理得:BC=2
,
在△ABC和△EFD中,
∵
,
∴△ABC≌△EFD(SSS).
故答案为:(1)
;2
 解:(1)延长AB,过C作CG⊥AB,交延长线于点G,
解:(1)延长AB,过C作CG⊥AB,交延长线于点G,在Rt△ACG中,CG=2,AG=4,
根据勾股定理得:AC=
| AG2+GC2 |
| 5 |
tanA=
| CG |
| AG |
| 1 |
| 2 |
(2)图中找出一点D,连接DE、DF,△ABC≌△EFD,如右图所示,
证明:在Rt△EMD中,EM=4,MD=2,
根据勾股定理得:ED=
| 42+22 |
| 5 |
在Rt△FDM中,FM=2,MD=2,
根据勾股定理得:FD=
| 22+22 |
| 2 |
同理在Rt△BCG中,根据勾股定理得:BC=2
| 2 |
在△ABC和△EFD中,
∵
|
∴△ABC≌△EFD(SSS).
故答案为:(1)
| 1 |
| 2 |
| 5 |
点评:此题考查了勾股定理,锐角三角函数定义,以及全等三角形的判定,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 (2012•河池)如图,已知AB为⊙O的直径,∠CAB=30°,则∠D的度数为( )
(2012•河池)如图,已知AB为⊙O的直径,∠CAB=30°,则∠D的度数为( )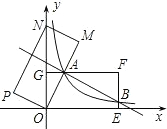 (2012•河池)如图,在平面直角坐标系中,矩形OEFG的顶点F的坐标为(4,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴上,得到矩形OMNP,OM与GF相交于点A.若经过点A的反比例函数
(2012•河池)如图,在平面直角坐标系中,矩形OEFG的顶点F的坐标为(4,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴上,得到矩形OMNP,OM与GF相交于点A.若经过点A的反比例函数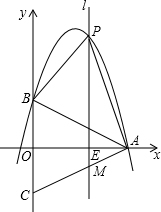 (2012•河池)如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=-
(2012•河池)如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=- (2012•河池)如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.若ED=5,则CE的长为( )
(2012•河池)如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.若ED=5,则CE的长为( ) (2012•河池)如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
(2012•河池)如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.