题目内容
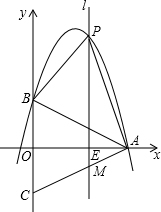 (2012•河池)如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=-
(2012•河池)如图,在等腰三角形ABC中,AB=AC,以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系,抛物线y=-| 1 |
| 2 |
| 7 |
| 2 |
(1)写出点A、点B的坐标;
(2)若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移,分别交线段OA、CA和抛物线于点E、M和点P,连接PA、PB.设直线l移动的时间为t(0<t<4)秒,求四边形PBCA的面积S(面积单位)与t(秒)的函数关系式,并求出四边形PBCA的最大面积;
(3)在(2)的条件下,抛物线上是否存在一点P,使得△PAM是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
分析:(1)抛物线的解析式中,令x=0,能确定点B的坐标;令y=0,能确定点A的坐标.
(2)四边形PBCA可看作△ABC、△PBA两部分;△ABC的面积是定值,关键是求出△PBA的面积表达式;若设直线l与直线AB的交点为Q,先用t表示出线段PQ的长,而△PAB的面积可由(
PQ•OA)求得,在求出S、t的函数关系式后,由函数的性质可求得S的最大值.
(3)△PAM中,∠APM是锐角,而PM∥y轴,∠AMP=∠ACO也不可能是直角,所以只有∠PAC是直角一种可能,即 直线AP、直线AC垂直,此时两直线的斜率乘积为-1,先求出直线AC的解析式,联立抛物线的解析式后可求得点P的坐标.
(2)四边形PBCA可看作△ABC、△PBA两部分;△ABC的面积是定值,关键是求出△PBA的面积表达式;若设直线l与直线AB的交点为Q,先用t表示出线段PQ的长,而△PAB的面积可由(
| 1 |
| 2 |
(3)△PAM中,∠APM是锐角,而PM∥y轴,∠AMP=∠ACO也不可能是直角,所以只有∠PAC是直角一种可能,即 直线AP、直线AC垂直,此时两直线的斜率乘积为-1,先求出直线AC的解析式,联立抛物线的解析式后可求得点P的坐标.
解答:解:(1)抛物线y=-
x2+
x+4中:
令x=0,y=4,则 B(0,4);
令y=0,0=-
x2+
x+4,解得 x1=-1、x2=8,则 A(8,0);
∴A(8,0)、B(0,4).
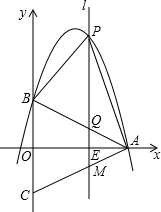 (2)△ABC中,AB=AC,AO⊥BC,则OB=OC=4,∴C(0,-4).
(2)△ABC中,AB=AC,AO⊥BC,则OB=OC=4,∴C(0,-4).
由A(8,0)、B(0,4),得:直线AB:y=-
x+4;
依题意,知:OE=2t,即 E(2t,0);
∴P(2t,-2t2+7t+4)、Q(2t,-t+4),PQ=(-2t2+7t+4)-(-t+4)=-2t2+8t;
S=S△ABC+S△PAB=
×8×8+
×(-2t2+8t)×8=-8t2+32t+32=-8(t-2)2+64;
∴当t=2时,S有最大值,且最大值为64.
(3)∵PM∥y轴,∴∠AMP=∠ACO<90°;
而∠APM是锐角,所以△PAM若是直角三角形,只能是∠PAM=90°;
由A(8,0)、C(0,-4),得:直线AC:y=
x-4;
所以,直线AP可设为:y=-2x+h,代入A(8,0),得:
-16+h=0,h=16
∴直线AP:y=-2x+16,联立抛物线的解析式,得:
,解得
、
∴存在符合条件的点P,且坐标为(3,10).
| 1 |
| 2 |
| 7 |
| 2 |
令x=0,y=4,则 B(0,4);
令y=0,0=-
| 1 |
| 2 |
| 7 |
| 2 |
∴A(8,0)、B(0,4).
 (2)△ABC中,AB=AC,AO⊥BC,则OB=OC=4,∴C(0,-4).
(2)△ABC中,AB=AC,AO⊥BC,则OB=OC=4,∴C(0,-4).由A(8,0)、B(0,4),得:直线AB:y=-
| 1 |
| 2 |
依题意,知:OE=2t,即 E(2t,0);
∴P(2t,-2t2+7t+4)、Q(2t,-t+4),PQ=(-2t2+7t+4)-(-t+4)=-2t2+8t;
S=S△ABC+S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
∴当t=2时,S有最大值,且最大值为64.
(3)∵PM∥y轴,∴∠AMP=∠ACO<90°;
而∠APM是锐角,所以△PAM若是直角三角形,只能是∠PAM=90°;
由A(8,0)、C(0,-4),得:直线AC:y=
| 1 |
| 2 |
所以,直线AP可设为:y=-2x+h,代入A(8,0),得:
-16+h=0,h=16
∴直线AP:y=-2x+16,联立抛物线的解析式,得:
|
|
|
∴存在符合条件的点P,且坐标为(3,10).
点评:此题主要考查的是函数图象与坐标轴的交点坐标的求法、图形面积的解法以及直角三角形的判定;最后一题中,先将不可能的情况排除掉可大大的简化解答过程.

练习册系列答案
相关题目
 (2012•河池)如图,已知AB为⊙O的直径,∠CAB=30°,则∠D的度数为( )
(2012•河池)如图,已知AB为⊙O的直径,∠CAB=30°,则∠D的度数为( )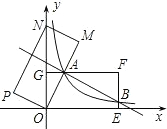 (2012•河池)如图,在平面直角坐标系中,矩形OEFG的顶点F的坐标为(4,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴上,得到矩形OMNP,OM与GF相交于点A.若经过点A的反比例函数
(2012•河池)如图,在平面直角坐标系中,矩形OEFG的顶点F的坐标为(4,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴上,得到矩形OMNP,OM与GF相交于点A.若经过点A的反比例函数 (2012•河池)如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.若ED=5,则CE的长为( )
(2012•河池)如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.若ED=5,则CE的长为( ) (2012•河池)如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
(2012•河池)如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.