题目内容
（2012•河池）如图，已知AB为⊙O的直径，∠CAB=30°，则∠D的度数为（ ）分析：由AB为⊙O的直径，根据直径所对的圆周角是直角，即可求得∠ACB=90°，又由∠CAB=30°，即可求得∠B的度数，然后由在同圆或等圆中，同弧或等弧所对的圆周角相等，即可求得∠D的度数．
解答：解：∵AB为⊙O的直径，
∴∠ACB=90°，
∵∠CAB=30°，
∴∠B=90°-∠CAB=60°，
∴∠D=∠B=60°．
故选C．
∴∠ACB=90°，
∵∠CAB=30°，
∴∠B=90°-∠CAB=60°，
∴∠D=∠B=60°．
故选C．
点评：此题考查了圆周角定理．此题难度不大，注意掌握直径所对的圆周角等于直角与在同圆或等圆中，同弧或等弧所对的圆周角相等定理的应用是解此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
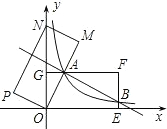（2012•河池）如图，在平面直角坐标系中，矩形OEFG的顶点F的坐标为（4，2），将矩形OEFG绕点O逆时针旋转，使点F落在y轴上，得到矩形OMNP，OM与GF相交于点A．若经过点A的反比例函数
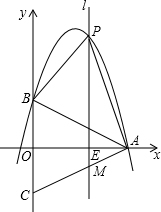（2012•河池）如图，在等腰三角形ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=-
（2012•河池）如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于E，垂足为D．若ED=5，则CE的长为（ ）
（2012•河池）如图，已知AB是⊙O的直径，⊙O过BC的中点D，且DE⊥AC于点E．