题目内容
如图1,在平面直角坐标系中,有一张矩形纸片OABC,已知O(0,0),A(8,0),C(0,4),点P是OA边上的动点(与点O、A不重合),将△PAB沿PB翻折,得到△PDB,
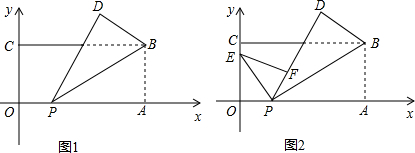
(Ⅰ)如图1,当∠BPA=30°时,求点D的坐标;
(Ⅱ)现在OC边上选取适当的点E,再将△POE沿PE翻折,得到△PEF.并使直线PD、PF重合.如图2,设P(x,0),E(0,y),求y关于x的函数关系式,并求y的最大值;
(Ⅲ)在(Ⅱ)的条件下,当点F恰好落在边CB上时,求点P的坐标.(直接写出结果即可).

(Ⅰ)如图1,当∠BPA=30°时,求点D的坐标;
(Ⅱ)现在OC边上选取适当的点E,再将△POE沿PE翻折,得到△PEF.并使直线PD、PF重合.如图2,设P(x,0),E(0,y),求y关于x的函数关系式,并求y的最大值;
(Ⅲ)在(Ⅱ)的条件下,当点F恰好落在边CB上时,求点P的坐标.(直接写出结果即可).
练习册系列答案
相关题目
菱形具有而矩形不一定具有的性质是( )
| A、内角和等于360° | B、对角相等 | C、对边平行且相等 | D、对角线互相垂直 |
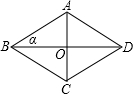 如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=a,则下列结论正确的是( )
如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=a,则下列结论正确的是( )A、sina=
| ||
B、cosa=
| ||
C、tana=
| ||
| D、以上都不正确 |
一组数据2,7,6,3,4,7的众数和中位数分别是( )
| A、7和4.5 | B、4和6 | C、7和4 | D、7和5 |

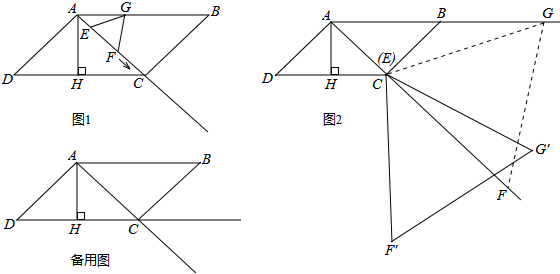
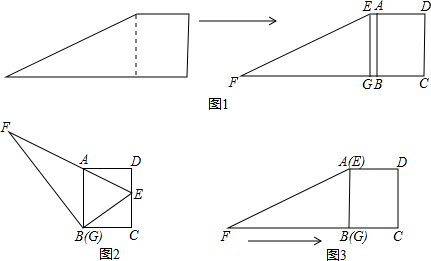
 如图①,在菱形ABCD中,AD=BD=1,现将△ABD沿AC方向向右平移到△A′B′D′的位置,得到图②,则阴影部分的周长为( )
如图①,在菱形ABCD中,AD=BD=1,现将△ABD沿AC方向向右平移到△A′B′D′的位置,得到图②,则阴影部分的周长为( )