题目内容
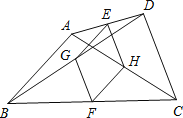
【题目】如图,在四边形ABCD中,AB=DC,E、F分别是AD、BC的中点,G、H分别是对角线BD、AC的中点.

(1)求证:四边形EGFH是菱形;
(2)若AB=1,则当∠ABC+∠DCB=90°时,求四边形EGFH的面积.
【答案】(1)见解析;(2)![]()
【解析】
试题分析:(1)利用三角形的中位线定理可以证得四边形EGFH的四边相等,即可证得;
(2)根据平行线的性质可以证得∠GFH=90°,得到菱形EGFH是正方形,利用三角形的中位线定理求得GE的长,则正方形的面积可以求得.
(1)证明:∵四边形ABCD中,E、F、G、H分别是AD、BC、BD、AC的中点,
∴FG=![]() CD,HE=
CD,HE=![]() CD,FH=
CD,FH=![]() AB,GE=
AB,GE=![]() AB.
AB.
∵AB=CD,
∴FG=FH=HE=EG.
∴四边形EGFH是菱形.
(2)解:∵四边形ABCD中,G、F、H分别是BD、BC、AC的中点,
∴GF∥DC,HF∥AB.
∴∠GFB=∠DCB,∠HFC=∠ABC.
∴∠HFC+∠GFB=∠ABC+∠DCB=90°.
∴∠GFH=90°.
∴菱形EGFH是正方形.
∵AB=1,
∴EG=![]() AB=
AB=![]() .
.
∴正方形EGFH的面积=(![]() )2=
)2=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目