��Ŀ����
����Ŀ�������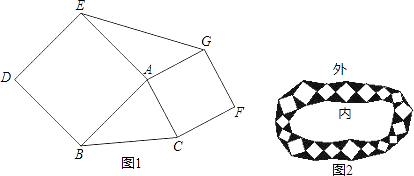
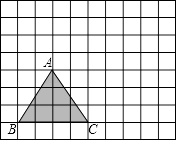
��1����ͼ1���ԡ�ABC�ı�AB��ACΪ�߷ֱ�������������ABDE��������ACFG������EG�����жϡ�ABC���AEG���֮��Ĺ�ϵ����˵�����ɣ�
��2����С·������ͨ�ģ���ͼ2��ʾ��С·�ɰ�ɫ����������ʯ�ͺ�ɫ����������ʯ�̳ɣ���֪�м�����������ε����֮����aƽ���ף���Ȧ�����������ε����֮����bƽ���ף�����С·һ��ռ�ض���ƽ���ף�
���𰸡�
��1��
�⣺��ABC���AEG�����ȣ�
���ɣ�����C��CM��AB��M������G��GN��EA��EA�ӳ�����N�����AMC=��ANG=90�㣬
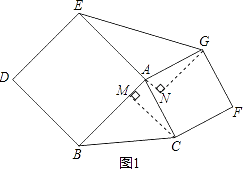
���ı���ABDE���ı���ACFG���������Σ�
���BAE=��CAG=90�㣬AB=AE��AC=AG��
�ߡ�BAE+��CAG+��BAC+��EAG=360�㣬
���BAC+��EAG=180�㣬
�ߡ�EAG+��GAN=180�㣬
���BAC=��GAN��
�ڡ�ACM�͡�AGN�У�
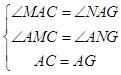 ��
��
���ACM�ա�AGN��
��CM=GN��
��S��ABC= ![]() ABCM��S��AEG=
ABCM��S��AEG= ![]() AEGN��
AEGN��
��S��ABC=S��AEG
��2��
�⣺�ɣ�1��֪��Ȧ�����������ε����֮�͵�����Ȧ�����������ε����֮�ͣ�
������С·�����Ϊ��a+2b��ƽ���ף�
����������1������C��CM��AB��M������G��GN��EA��EA�ӳ�����N���ó���ABC���AEG�������ߣ��������ε�������֤����ACM�ա�AGN�����жϡ�ABC���AEG���֮��Ĺ�ϵ�Ĺؼ�����2��ͬ��1������֪��Ȧ�����������ε����֮�͵�����Ȧ�����������ε����֮�ͣ��������С·һ��ռ�ض���ƽ���ף�

����Ŀ��С��ͬѧ�μ���ĩ���ʵ�����������ƽ���硱�߲˴������ռ���20������������С�������ĸ�����
32 39 45 55 60 54 60 28 56 41
51 36 44 46 40 53 37 47 45 46
��1���������õĵ��鷽���� ��
��2��������20���������Ϊ8���з��飬�벹ȫƵ���ֲ�����Ƶ���ֲ�ֱ��ͼ
�������� | 28��x��36 | 36��x��44 | 44��x��52 | 52��x��60 | 60��x��68 |
Ƶ�� | 2 | 2 |
��3��ͨ��Ƶ���ֲ�ֱ��ͼ�Է����˴������������ij��ƣ�
����Ŀ������ij��ѧ���С��й���У�����������ִ������ߡ����в����ݳ����ɼ�����ѡ��5��ѡ����ɳ��д����Ӻ��д����Ӳμ�ѧУ�����������Ӹ�ѡ����5��ѡ�ֵľ����ɼ���ͼ��ʾ��
ƽ���֣��֣� | ��λ�����֣� | �������֣� | |
���в� | 85 | ||
���в� | 85 | 100 |

��1������ͼʾ��д����
��2��������ӳɼ���ƽ��������λ�����з������ĸ��ӵľ����ɼ��Ϻã�
��3���������Ӿ����ɼ��ķ�����ж���һ��������ѡ�ֳɼ���Ϊ�ȶ���