��Ŀ����
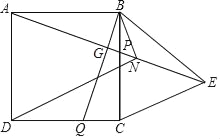
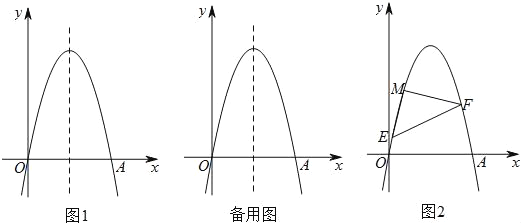
����Ŀ����ͼ1��������y=��x2+6x��x�ύ��O��A���㣬��P���������ϣ�����P��ֱ��y=x+m�������ߵĶԳ��ύ�ڵ�Q��
��1�����������ߵĶԳ����ǣ�ֱ���� ����ֱ��PQ��x��������ǵĶ������� ���ȣ�
��2����S��POQ��S��PAQ=1��2�����ʱ�ĵ�P���ꣻ
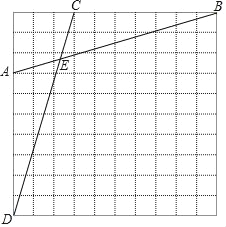
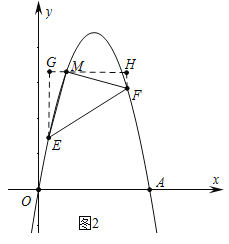
��3����ͼ2����M��1��5�����������ϣ��Ե�MΪֱ�Ƕ�����Rt��MEF����E��F�����������ϣ�����������������ֱ��EF��Ȼ��������N�����N���꣮
���𰸡���1��x=3��45��2����2��8����3��9����3��ֱ��EF������N��5��4��
��������
��1�����������ߵĶԳ��ṫʽ���㼴��������ֱ��y=x+m��ֱ��y=xƽ�пɵý�����
��2����ͼ1������ֱ��y=x���Գ�����H������AH���ӳ�AH��ֱ��PQ��M����ON��PQ��N���ı���ONMH�Ǿ��Σ���AOH�ǵ���ֱ�������Σ���S��POQ��S��PAQ=1��2���Ƴ�AM=2ON��ON=MH=AH���ɵ�A��6��0����H��3��3�����Ƴ���M��0��6���������ֱ��PQ�����÷����鼴�ɽ��������
��3����ͼ2��������M��GH��OA������E��EG��GH��G������F��FH��GH��H���ɡ�EMG�ס�MFH����![]() =
=![]() ����E��x1��y1����F��x2��y2����ֱ��EF�Ľ���ʽΪy=mx+n����
����E��x1��y1����F��x2��y2����ֱ��EF�Ľ���ʽΪy=mx+n����![]() =
=![]() ����y1=��x12+6x1��y2=��x22+6x2������ʽ�����õ�x1x2��5��x1+x2��+26=0���г������������ø���ϵ����ϵ���m��n�Ĺ�ϵ���ɽ��������
����y1=��x12+6x1��y2=��x22+6x2������ʽ�����õ�x1x2��5��x1+x2��+26=0���г������������ø���ϵ����ϵ���m��n�Ĺ�ϵ���ɽ��������
��1��������y=��x2+6x�ĶԳ���x=��![]() =3��
=3��
��ֱ��PQ��y=x+m��ֱ��y=xƽ����ֱ��y=x��һ��������ƽ��������ֱ��PQ��x��������ǵĶ�����45�㣮
�ʴ�Ϊ��x=3��45��
��2����ͼ1������ֱ��y=x���Գ�����H������AH���ӳ�AH��ֱ��PQ��M����ON��PQ��N���ı���ONMH�Ǿ��Σ���AOH�ǵ���ֱ����������
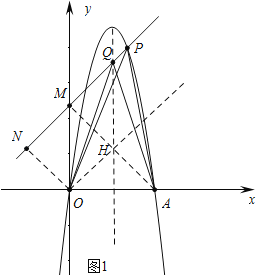
��S��POQ��S��PAQ=1��2����AM=2ON����ON=MH=AH��
�ߵ�A��6��0����H��3��3�������M��0��6������ֱ��PQ�Ľ���ʽΪy=x+6����![]() �������
�������![]() ��
��![]() �����P���꣨2��8����3��9����
�����P���꣨2��8����3��9����
��3����ͼ2��������M��GH��OA������E��EG��GH��G������F��FH��GH��H��
�ߡ�EMF=90�㣬���EMG+��FMH=90�㣮
�ߡ�FMH+��MFH=90�㣬���EMG=��MFH��
�ߡ�G=��H=90�㣬���EMG�ס�MFH����![]() =
=![]() ��
��
��E��x1��y1����F��x2��y2����ֱ��EF�Ľ���ʽΪy=mx+n��
��EM��MF����![]() =
=![]() ��
��
��y1=��x12+6x1��y2=��x22+6x2������ʽ�����õ�x1x2��5��x1+x2��+26=0
��![]() ��ȥy�õ���x2+��m��6��x+n=0����x1+x2=6��m��x1x2=n����n��5��6��m��+26=0����n=4��5m����ֱ��EF����ʽΪy=mx+4��5m=��x��5��m+4����x=5ʱ��y=4����ֱ��EF������N��5��4����
��ȥy�õ���x2+��m��6��x+n=0����x1+x2=6��m��x1x2=n����n��5��6��m��+26=0����n=4��5m����ֱ��EF����ʽΪy=mx+4��5m=��x��5��m+4����x=5ʱ��y=4����ֱ��EF������N��5��4����

 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�����Ŀ�����ݹ���ʵ�еġ�����ѧ�����ʽ����������Ի�������һѧ�����߽��г������飬�Ա��ܽỳ������һѧ���ִ���������⣬������Ӱ�����أ�Ϊѧ���Ľ�����չ��ѧУ���������ĸ����������飮��֪��������һѧ��������840�ˣ�Ů��800�ˣ����ǵ�������150��x��175��Χ�ڣ������ȡ��һѧ�����г������飮��ȡ�������У�������Ů����2�ˣ������������ݻ�������ͳ��ͼ����

������������
��� | ���ߣ�cm�� |
A | 150��x��155 |
B | 155��x��160 |
C | 160��x��165 |
D | 165��x��170 |
E | 170��x��175 |
����ͳ��ͼ���ṩ����Ϣ������˵����
�ٳ�ȡ�����������У�������155��x��165֮���ѧ����18�ˣ�
�ڳ�һѧ����Ů�������ߵ���λ����B�飻
�۳�ȡ�������У���ȡŮ��������������38��
�ܳ�һѧ��������160��x��170֮���ѧ��Լ��800�ˣ�
���к������ǣ�������
A.�٢�B.�٢�C.�ڢ�D.�ۢ�
����Ŀ��һ��Ҷר���꾭��ij��Ʒ�ƵIJ�Ҷ���ò�Ҷ�ijɱ�����80Ԫ/kg�����۵��۲�����120Ԫ/kg���Ҳ�����180Ԫ/kg������һ��ʱ���õ��������ݣ�
���۵���x��Ԫ/kg�� | 120 | 130 | �� | 180 |
ÿ������y��kg�� | 100 | 95 | �� | 70 |
��y��x�Ĺ�ϵ��������ѧ����ijһ�ֺ�����ϵ��
��1��ֱ��д��y��x�ĺ�����ϵʽ����ָ���Ա���x��ȡֵ��Χ��
��2�������۵���Ϊ����ʱ���������������������Ƕ��٣�
����Ŀ��ijũ��������ͬ��������ij���������ӷ�ѿ�ʵ����飬������±���ʾ��
���Ӹ���n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
��ѿ���Ӹ���m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
��ѿ����Ƶ�� | 0��899 | 0��910 | 0��898 | 0��911 | 0��909 | 0��912 | 0��908 | 0��910 |
һ��أ�![]() �������������д�Լ�ж����Dz��ܷ�ѿ�ģ�
�������������д�Լ�ж����Dz��ܷ�ѿ�ģ�