Question

【题目】在△ABC中，D、E分别是AB,AC的中点，作∠B的角平分线

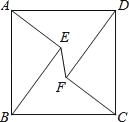
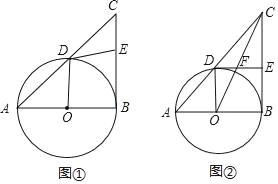
（1）如图1，若∠B的平分线恰好经过点E，猜想△ABC是怎样的特殊三角形，并说明理由；

（2）如图2，若∠B的平分线交线段DE于点F，已知AB=8，BC=10，求EF的长度；

（3）若∠B的平分线交直线DE于点F，直接写出AB、BC、EF三者之间的数量关系。

Answer 1

【答案】（1）△ABC是等腰三角形，理由见解析；

（2）EF=CG =1；

（3）EF=

【解析】

试题（1）由三角形中位线的性质得DE∥BC，∠DEB=∠EBC，由BE平分∠ABC，得DE=DB，∠A=∠DEA，所以∠DEB+∠DBE+∠A+∠DEA=180°，∠AEB=90°，故△ABC是等腰三角形；（2）连接AF并延长交BC于点G，由DE∥BC，BF平分∠ABC，∠DFB=∠FBC，再由角边角得出△ABF≌△GBF，CG=2，由AE=CE得出EF =1；（3）分两种情况讨论.

试题解析：（1）△ABC是等腰三角形。

理由：∵D、E分别是AB,AC的中点，

∴DE∥BC ∴ ∠DEB=∠EBC，

∵BE平分∠ABC

∴∠DBE=∠EBC

∴∠DEB=∠DBE

∴ DE=DB

∵DE=DB=DA

∴∠A=∠DEA

∴∠DEB+∠DBE+∠A+∠DEA=180°

∴∠AEB=90°即BE垂直平分AC

∴BA=BC 即△ABC是等腰三角形

（2）连接AF并延长交BC于点G

∵D、E分别是AB,AC的中点

∴DE∥BC

∴ ∠DFB=∠FBC

∵BF平分∠ABC

∴∠DBF=∠FBC

∴∠DFB=∠DBF

∴ DF=DB

∵DF=DB=DA

∴∠DAF=∠DFA

∴∠DFB+∠DBF+∠DAF+∠DFA=180°

∴∠AFB=∠GFB=90°,BF=BF, ∠ABF=∠GBF

∴△ABF≌△GBF AB=GB=8,AF=GF

∴ CG=BC-BG=2

又AE=CE

∴EF=CG =1

(3) ①

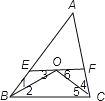
如图,∵EF∥BC,

∴∠2=∠3，

又∵∠1=∠2，

∴∠1=∠3，

∴OE=BE，

在△CFO中，同理可证OF=CF，

∵EF=EO+FO，

∴EF=BE+CF；

②

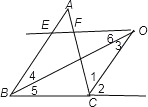
如图,∵OE∥BC,

∴∠5=∠6，

又∠4=∠5，

∴∠4=∠6，

∴OE=BE，

在△CFO中，同理可证OF=CF，

∵EF=EOFO，

∴EF=BECF.

综上：EF=