Question

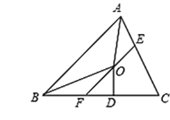
【题目】如图，在△ABC中，∠BAC和∠ABC的平分线相交于点O，过点O作EF∥AB交BC于点F，交AC于点E，过点O作OD⊥BC于D，下列四个结论：①∠AOB=90°+∠C；②AE+BF=EF；③当∠C=90°时，E、F分别是AC、BC的中点；④若OD=CE+CF=则S△CEF=,其中正确的是______________

Answer 1

【答案】①②④

【解析】

根据三角形的内角和定理可得∠BAC+∠ABC=180°-∠C，再根据角平分线的定义可得∠OAB+∠OBA=（∠BAC+∠ABC），然后根据三角形的内角和定理列式整理即可得解，判断出①正确；由平行线的性质和角平分线的定义得出△BFO和△AEO是等腰三角形得出AE+BF=EF故②正确；根据角平分线的定义判断出点O在∠ACB的平分线上，从而得到点O不是∠ACB的平分线的中点，然后判断出③错误；根据角平分线上的点到角的两边距离相等可得点O到AC的距离等于OD，再利用三角形的面积公式列式计算即可得到S△CEF=ab，判断出④正确．

在△ABC中，∠BAC+∠ABC=180°-∠C，

∵∠BAC和∠ABC的平分线相交于点O，

∴∠OAB+∠OBA=（∠BAC+∠ABC）=90°-∠C，

在△AOB中，∠AOB=180°-（90°-∠C）=90°+∠C，故①正确；

∵在△ABC中，∠BAC和∠ABC的平分线相交于点O，

∴∠OBC=∠OBA，∠OAE=∠OAB，

∵EF∥AB，

∴∠OBA=∠BOF，∠BAO=∠AOE，

∴∠BOF=∠FBO，∠OAE=∠AOE，

∴FB=FO，EO=EA，

∴EF=OE+OF=BF+AE，

故②正确；

∵∠BAC和∠ABC的平分线相交于点O，

∴点O在∠ACB的平分线上，

∴点O不是∠ACB的平分线的中点，

∵EF∥AB，

∴E，F一定不是AC，BC的中点，故③错误；

∵点O在∠ACB的平分线上，

∴点O到AC的距离等于OD，

∴S△CEF=（CE+CF）OD=×2ba=ab，故④正确；

综上所述，正确的是①②④

故答案为：①②④．