题目内容
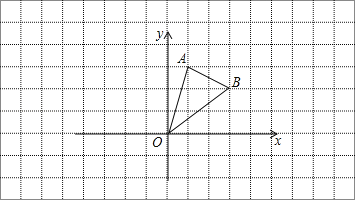
【题目】如图,已知在平面直角坐标系中,A(0,﹣1)、B(﹣2,0)C(4,0)
(1)求△ABC的面积;
(2)在y轴上是否存在一个点D,使得△ABD为等腰三角形,若存在,求出点D坐标;若不存,说明理由.

【答案】(1)3;(2)存在,点D坐标为(0,![]() ),(0,-1-
),(0,-1-![]() ),(0,1).
),(0,1).
【解析】
(1)根据AO=1,BC=6,求得△ABC的面积;
(2)分AB为底边和腰两种情况进行分类讨论,i)以AB为底边,设D(0,a),则AD=1+a,OD=a,根据BD=AD=1+a,∠BOD=90°,可得Rt△BOD中,OD2+OB2=BD2,即a2+22=(a+1)2,进而得出点D坐标;ii)以AB为腰,求出AB的长,在y轴即可确定点D的坐标.
(1)∵A(0,-1)、B(-2,0)、C(4,0),
∴AO=1,BC=6,
∴△ABC的面积=![]() ×6×1=3;
×6×1=3;
(2)存在一个点D,使得△ABD是等腰三角形.
i)如图所示,以AB为底边,
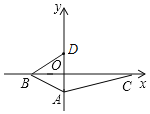
设D(0,a),则AD=1+a,OD=a,
∵BD=AD=1+a,∠BOD=90°,
∴Rt△BOD中,OD2+OB2=BD2,
∴a2+22=(a+1)2,
解得a=![]() ,
,
∴D(0,![]() );
);
ii) 如图所示,以AB为腰,

∵A(0,﹣1)、B(﹣2,0)
∴BO=2,AO=1,
∵∠BOA=90゜
∴AB=![]() ,
,
若AB=AD,则有AD=![]()
∴D点坐标为(0,-1-![]() ),
),
若AB=BD,则OD=OA=1,
∴D点坐标为(0,1).
故存在一个点D,使得△ABD是等腰三角形.D点坐标为(0,![]() ),(0,-1-
),(0,-1-![]() ),(0,1).
),(0,1).

【题目】我市自开展“学习新思想,做好接班人”主题阅读活动以来,受到各校的广泛关注和同学们的积极响应,某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7及以上 |
人数(人) | 20 | 28 | m | 16 | 12 |

请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和![]() 的值;
的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果估计该校学生在这一周内文章阅读的篇数为4篇的人数.