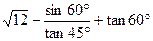题目内容
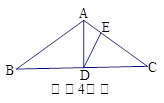
如图，已知AD是等腰△ABC底边上的高，且tan∠B=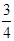
，AC上有一点E满足AE∶CE= 2∶3，则tan∠ADE的值是（ ）
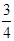，AC上有一点E满足AE∶CE= 2∶3，则tan∠ADE的值是（ ）A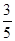． | B． | C． | D． |
B
|
解：如图设AD=3a，因为AD是等腰△ABC底边上的高，且tan∠B=
，得BD=DC=4a 所以AB=5a进而AC="5a" 又AE∶CE= 2∶3故AE=2a EC=3a
过E点作EF∥BC
EF与底边BC上的高AD相交与G,
因为EF∥BC 所以AG∶AD=EG∶DC=AE∶AC=2∶5
所以EG=
a 
a 故GD=
a在Rt△EGD中，tan∠ADE=EG/GD=
故选B
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
的边OA上一点，且P点的坐标为（3，4），则sin
，再往摩天轮的方向前进50 m至D处，测得最高点A的仰角为
．求该兴趣小组测得的摩天轮的高度AB
BC，则∠A的度数是 ，cosB= 
,则∠Ａ＝ 