题目内容
【题目】当我们利用2种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2 . 
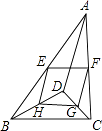
(1)由图2,可得等式: .
(2)利用(1)中所得到的结论,解决下面的问题:
已知 a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)利用图3中的纸片(足够多),画出一种拼图,使该拼图可用来验证等式:2a2+5ab+2b2=(2a+b)(a+2b);
(4)小明用2 张边长为a 的正方形,3 张边长为b的正方形,5 张边长分别为a、b 的长方形纸片重新拼出一个长方形,那么该长方形较长的一条边长为 .
【答案】
(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
(2)
解:
∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2=(a+b+c)2﹣2(ab+ac+bc)=121﹣76=45;
(3)
解:
如图所示:

(4)2a+3b
【解析】(1)根据图2,利用直接求与间接法分别表示出正方形面积,即可确定出所求等式;
(2)根据(1)中结果,求出所求式子的值即可;
(3)根据已知等式,做出相应图形,如图所示;
(4)根据题意列出关系式,即可确定出长方形较长的边.
【考点精析】认真审题,首先需要了解多项式乘多项式(多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加).

练习册系列答案
相关题目