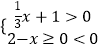题目内容
【题目】如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了5 ![]() km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点.
km到达B点,然后再沿北偏西30°方向走了5km到达目的地C点. 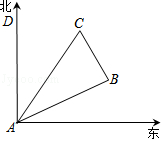
(1)求A、C两点之间的距离;
(2)确定目的地C在营地A的什么方向上.
【答案】
(1)解:过B点作直线EF∥AD
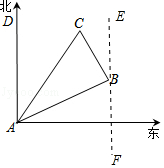 ,
,
∴∠DAB=∠ABF=60°,
∵∠EBC=30°,
∴∠ABC=180°﹣∠ABF﹣∠EBC=180°﹣60°﹣30°=90°,
∴△ABC为直角三角形,由已知可得:BC=5km,AB=5 ![]() km,
km,
由勾股定理可得:AC2=BC2+AB2,
所以AC= ![]() =10(km),
=10(km),
即:A、C两点之间的距离为10km
(2)解:在Rt△ABC中,∵BC=5km,AC=10km,
∴∠CAB=30°,
∵∠DAB=60°,
∴∠DAC=30°,
即点C在点A的北偏东30°的方向上
【解析】(1)根据平行线的性质,可得∠ABF,根据直角三角形的判定,可得∠ABC,根据勾股定理,可得答案;(2)根据直角三角形的性质,可得∠CAB,根据角的和差,可得答案.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
【题目】如图所示的日历中,任意圈出一竖列相邻的三个数,设中间一个数为a,则这三个数之和为(用含a的式子表示)
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | |||
5 | 6 | 7 | 8 | 9 | 10 | 11 |
12 | 13 | 14 | 15 | 16 | 17 | 18 |
19 | 20 | 21 | 22 | 23 | 24 | 25 |
26 | 27 | 28 | 29 | 30 | 31 |