题目内容
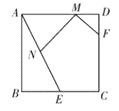
【题目】如图,在正方形ABCD中,AB=4,E是BC边的中点, F是CD边上的一点, 且DF=1.若M、N分别是线段AD、AE上的动点,则MN+MF的最小值为________.
【答案】![]()
【解析】
作点F关于AD的对称点G,过点G作GN⊥AE于点N,交AD于点M,可证得MG=MF,△MDG≌△MDF,DF=DG=1 ,可推出MN+MF=NG,根据垂线段最短,可知此时MN+MF的最小值就是NG的长;利用正方形的性质,可求出BE的长,同时可以推出∠B=∠ANM=∠FDM,∠AMN=∠BAE=∠FMD,再利用有两组对应角相等的三角形相似,可证得△ABE∽△MNA∽△FMD,然后利用相似三角形的性质及勾股定理就可求出MN,MG的长,由此看求出NG的长.
作点F关于AD的对称点G,过点G作GN⊥AE于点N,交AD于点M,
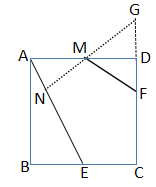
∴MG=MF,△MDG≌△MDF,DF=DG=1
∴∠GMD=∠DMF
∴MN+MF=MN+MG=NG
根据垂线段最短,可知此时MN+MF的最小值就是NG的长.
∵正方形BCD,点E是BC的中点
∴BE=![]() BC=
BC=![]() AB=2
AB=2
∴∠B=∠ANM=∠FDM=90°,∠BAE+∠MAN=90°,
∵∠AMN+∠MAN=90°,
∴∠AMN=∠BAE,
∵∠AMN=∠DMG
∴∠AMN=∠BAE=∠FMD
∴△ABE∽△MNA∽△FMD
∴![]() 即
即![]()
解之:MD=2,
∴AM=AD-MD=4-2=2
∴![]()
设AN=x,则MN=2x
∴AN2+MN2=AM2,
∴x2+4x2=4
解之:AN=x=![]()
∴MN=2AN=![]() ;
;
在Rt△MDG中,MG=![]()
∴NG=MN+MG=![]() .
.
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目