题目内容
【题目】某公司分两次采购甲、乙两种商品,具体情况如下:
商品 | 甲 | 乙 | 花费资金 |
次数 | |||
第一次采购件数 | 10件 | 15件 | 350元 |
第二次采购件数 | 15件 | 10件 | 375元 |
(1)求甲、乙商品每件各多少元?
(2)公司计划第三次采购甲、乙两种商品共31件,要求花费资金不超过475元,问最多可购买甲商品多少件?
【答案】(1)甲商品每件17元,乙商品每件12元;(2)最多可购买甲商品20件
【解析】
(1)设甲商品每件x元,乙商品每件y元,构建方程组即可解决问题;
(2)设购买甲商品a件.根据不等式即可解决问题;
解:(1)设甲商品每件x元,乙商品每件y元.
由题意![]() ,
,
解得![]() ,
,
答:甲商品每件17元,乙商品每件12元.
(2)设购买甲商品a件.
由题意:17a+12(31-a)≤475,
解得a≤20.6,
∵a是整数,
∴最多可购买甲商品20件,
答:最多可购买甲商品20件.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案【题目】某学习小组在学习了函数及函数图象的知识后,想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大. 请将他们的探究过程补充完整.
(1)列函数表达式:若矩形的周长为8,设矩形的一边长为x,面积为y,则有y=____________;
(2)上述函数表达式中,自变量x的取值范围是____________;
(3)列表:
x | … | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
y | … | 1.75 | 3 | 3.75 | 4 | 3.75 | 3 | m | … |
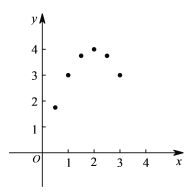
写出m=____________;
(4)画图:在平面直角坐标系中已描出了上表中部分各对应值为坐标的点,请你画出该函数的图象;
(5)结合图象可得,x=____________时,矩形的面积最大;写出该函数的其它性质(一条即可):____________.
【题目】为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如表:
天数(x) | 1 | 3 | 6 | 10 |
每件成本p(元) | 7.5 | 8.5 | 10 | 12 |
任务完成后,统计发现工人李师傅第x天生产的产品件数y(件)与x(天)满足如下关系:y=![]() ,
,
设李师傅第x天创造的产品利润为W元.
(1)直接写出p与x,W与x之间的函数关系式,并注明自变量x的取值范围:
(2)求李师傅第几天创造的利润最大?最大利润是多少元?
(3)任务完成后.统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金.请计算李师傅共可获得多少元奖金?