题目内容
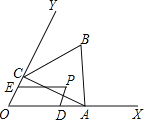
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.
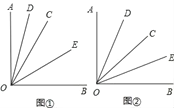
(1)如图①,当∠BOC=40°时,求∠DOE的度数;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠DOE的大小是否发生变化,说明理由;
(3)当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时,画出图形,直接写出∠DOE的度数(不必写过程).
【答案】(1)45°;(2)∠DOE的大小不变,理由见解析;(3)45°或135°;画图见解析.
【解析】
(1)如图①,当∠BOC=40°时,求∠DOE的度数;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠DOE的大小是否发生变化,说明理由;
(3)当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时,画出图形,直接写出相应的∠DOE的度数(不必写出过程).
解:(1)如图,∠AOC=90°﹣∠BOC=50°,
∵OD、OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC=25°,∠COE=
∠AOC=25°,∠COE=![]() ∠BOC=20°,
∠BOC=20°,
∴∠DOE=∠COD+∠COE=45°;
(2)∠DOE的大小不变,理由是:
∠DOE=∠COD+∠COE=![]() ∠AOC+
∠AOC+![]() ∠COB=
∠COB=![]() (∠AOC+∠COB)=
(∠AOC+∠COB)=![]() ∠AOB=45°;
∠AOB=45°;
(3)∠DOE的大小发生变化情况为,
如图3,则∠DOE为45°;如图4,则∠DOE为135°,
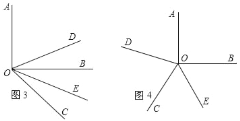
分两种情况:如图3所示,
∵OD、OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,
∠BOC,
∴∠DOE=∠COD﹣∠COE=![]() (∠AOC﹣∠BOC)=45°;
(∠AOC﹣∠BOC)=45°;
如图4所示,∵OD、OE分别平分∠AOC和∠BOC,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,
∠BOC,
∴∠DOE=∠COD+∠COE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ×270°=135°.
×270°=135°.

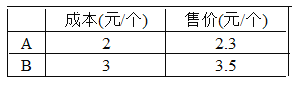
【题目】某公司分两次采购甲、乙两种商品,具体情况如下:
商品 | 甲 | 乙 | 花费资金 |
次数 | |||
第一次采购件数 | 10件 | 15件 | 350元 |
第二次采购件数 | 15件 | 10件 | 375元 |
(1)求甲、乙商品每件各多少元?
(2)公司计划第三次采购甲、乙两种商品共31件,要求花费资金不超过475元,问最多可购买甲商品多少件?