题目内容
【题目】在平面直角坐标系中,点A(-1,-2),B(5,4).已知抛物线y=x2-2x+c与线段AB有公共点,则c的取值范围是________.
【答案】-11≤c≤![]()
【解析】抛物线y=x2-2x+c与y轴的交点坐标为(0,c).
如解图,抛物线的对称轴为直线x=1,
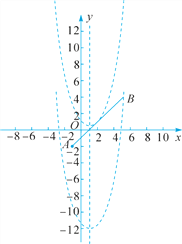
易求得直线AB的函数表达式为y=x-1.
当直线AB与抛物线y=x2-2x+c只有一个公共点,即方程x2-2x+c=x-1的Δ=0时,抛物线y=x2-2x+c与y轴的交点最高,即c的值最大,此时9-4(c+1)=0,解得c=![]() .
.
当抛物线y=x2-2x+c过点B时,抛物线y=x2-2x+c与y轴的交点最低,即c的值最小,
把点B(5,4)的坐标代入y=x2-2x+c,得25-10+c=4,解得c=-11.
∴C的取值范围是-11≤c≤![]() .
.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目