题目内容
【题目】如图,已知反比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象关于
的图象关于![]() 轴对称,
轴对称,![]() ,
,![]() 是函数
是函数![]() 图象上的两点,连接
图象上的两点,连接![]() ,点
,点![]() 是函数
是函数![]() 图象上的一点,连接
图象上的一点,连接![]() ,
,![]() .
.
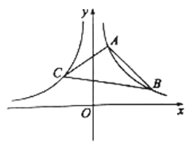
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 所在直线的表达式;
所在直线的表达式;
(3)求![]() 的面积.
的面积.
【答案】(1)m=1,n=2.(2)y=-x+5;(3)![]()
【解析】分析: (1)先把A点坐标代入![]() 得k1=4,则反比例函数解析式为y=
得k1=4,则反比例函数解析式为y=![]() (x>0),再利用反比例解析式确定B点坐标即可求出m的值,根据两个反比例函数的图象关于
(x>0),再利用反比例解析式确定B点坐标即可求出m的值,根据两个反比例函数的图象关于![]() 轴对称,可得k=-4,又由点
轴对称,可得k=-4,又由点![]() 是函数
是函数![]() 图象上的一点即可求出n的值;
图象上的一点即可求出n的值;
(2)根据A,B两点坐标利用待定系数法即可求出一次函数解析式.
(3)自A,B,C三点分别向x轴作垂线,垂足分别为A′,B′,C′,然后根据三角形面积公式和![]() 进行计算.
进行计算.
详解:
(1)由A(1,4),B(4,m)是函数![]() (x>0)图象上的两点,
(x>0)图象上的两点,
∴4=![]() ,k1=4,
,k1=4,
∴![]() (x>0)
(x>0)
∴m=![]() .
.
∵![]() (x<0)的图象和
(x<0)的图象和![]() (x>0)的图象关于y轴对称,
(x>0)的图象关于y轴对称,
∴点A(1,4)关于y轴的对称点A1(-1,4)在![]() (x<0)的图象上,
(x<0)的图象上,
∴4=![]() ,k2=-4,
,k2=-4,
∴![]()
由点C(-2,n)是函数![]() 图象上的一点,
图象上的一点,
∴n=2.
(2设AB所在直线的表达式为y=kx+b,
将A(1,4),B(4,1)分别代入y=kx+b,得![]()
解这个二元一次方程组,得![]() .
.
∴AB所在直线表达式为:y=-x+5
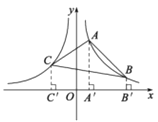
(3)自A,B,C三点分别向x轴作垂线,垂足分别为A′,B′,C′,
CC′=2,AA′=4,BB′=1,C′A′=3,A′B′=3,C′B′=6.
∴![]() ′
′
=![]() ×(2+4) ×3+
×(2+4) ×3+![]() ×(1+4) ×3-
×(1+4) ×3-![]() ×(2+1) ×6=
×(2+1) ×6=![]()

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】近期电影《少年的你》受到广大青少年的喜爱,某校七年级1班2班的几名同学请他们的家长在网上买票,家长了解到某电影院的活动,设购买电影票的张数为![]()
购买张数 |
|
|
|
每张票的价格 |
|
|
|
家长沟通后决定两个班的同学在期中考试结束后去观看。两个班共有![]() 人,期中
人,期中![]() 班人数多于
班人数多于![]() 不足
不足![]() 人。经过估算,如果两个班都以班为单位购买,则一共应付
人。经过估算,如果两个班都以班为单位购买,则一共应付![]() 元。
元。
![]() 求两个班有多少个同学?
求两个班有多少个同学?
![]() 如果两个班联合起来,作为一个团体购票,可以节省多少钱?
如果两个班联合起来,作为一个团体购票,可以节省多少钱?
![]() 如果七年级
如果七年级![]() 班同学作为一个团体购票,你认为如何购票才最省钱?可以节省多少钱?
班同学作为一个团体购票,你认为如何购票才最省钱?可以节省多少钱?