题目内容
 如图,在Rt△OAB中,∠OBA=90°,OB=AB=4,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
如图,在Rt△OAB中,∠OBA=90°,OB=AB=4,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.(1)线段OB1的长是
4
4
,∠A1OB的度数是135°
135°
;(2)连接BB1,求证:四边形OBB1A1是平行四边形;
(3)求四边形OBB1A1的面积.
分析:(1)根据旋转的性质得出BO=B1O,∠BOB1=90°,再根据角之间的关系得到∠A1OB的度数;
(2)根据旋转的性质易得A1B1=AB,∠OA1B1=∠A1OA=90°,从而证明四边形OAA1B1是平行四边形.
(3)利用平行四边形的面积计算公式可得答案.
(2)根据旋转的性质易得A1B1=AB,∠OA1B1=∠A1OA=90°,从而证明四边形OAA1B1是平行四边形.
(3)利用平行四边形的面积计算公式可得答案.
解答:(1)解:根据旋转可得:
BO=B1O,∠BOB1=90°,
∵OB=4,
∴BO=B1O=4,
∵∠OBA=90°,OB=AB=4,
∴∠AOB=45°,
根据旋转可得∠AOB=∠A1OB1=45°,
∴∠A1OB=45°+90°=135°;
(2)证明:∵∠BOB1=90°,∠A1B1O=90°,
∴A1B1∥OB,
∵A1B1=AB=BO,
∴四边形OBB1A1是平行四边形;
(3)解:∵BO=B1O=4,
∴四边形OBB1A1的面积为:4×4=16.
BO=B1O,∠BOB1=90°,
∵OB=4,
∴BO=B1O=4,
∵∠OBA=90°,OB=AB=4,
∴∠AOB=45°,
根据旋转可得∠AOB=∠A1OB1=45°,

∴∠A1OB=45°+90°=135°;
(2)证明:∵∠BOB1=90°,∠A1B1O=90°,
∴A1B1∥OB,
∵A1B1=AB=BO,
∴四边形OBB1A1是平行四边形;
(3)解:∵BO=B1O=4,
∴四边形OBB1A1的面积为:4×4=16.
点评:此题主要考查了旋转的性质,以及平行四边形的判定与面积计算,关键是旋转前后对应角相等,对应边相等.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
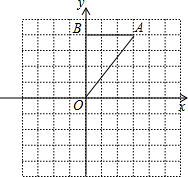 如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).
如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).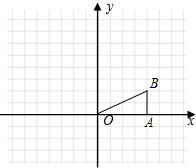 OA1B1.
OA1B1.
 (2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.