题目内容
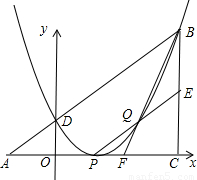
 (2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.(1)线段OA1的长是
6
6
,∠AOB1的度数是135
135
度;(2)连接AA1,求证:四边形OAA1B1是平行四边形;
(3)四边形OAA1B1的面积.
分析:(1)图形在旋转过程中,边长和角的度数不变;
(2)可证明OA∥A1B1且相等,即可证明四边形OAA1B1是平行四边形;
(3)平行四边形的面积=底×高=OA×OA1.
(2)可证明OA∥A1B1且相等,即可证明四边形OAA1B1是平行四边形;
(3)平行四边形的面积=底×高=OA×OA1.
解答:解:(1)因为,∠OAB=90°,OA=AB,
所以,△OAB为等腰直角三角形,即∠AOB=45°,
根据旋转的性质,对应点到旋转中心的距离相等,即OA1=OA=6,
对应角∠A1OB1=∠AOB=45°,旋转角∠AOA1=90°,
所以,∠AOB1的度数是90°+45°=135°;
(2)∵∠AOA1=∠OA1B1=90°∴OA∥A1B1,
又OA=AB=A1B1,
∴四边形OAA1B1是平行四边形.
(3)?OAA1B1的面积=6×6=36.
所以,△OAB为等腰直角三角形,即∠AOB=45°,
根据旋转的性质,对应点到旋转中心的距离相等,即OA1=OA=6,
对应角∠A1OB1=∠AOB=45°,旋转角∠AOA1=90°,
所以,∠AOB1的度数是90°+45°=135°;
(2)∵∠AOA1=∠OA1B1=90°∴OA∥A1B1,
又OA=AB=A1B1,
∴四边形OAA1B1是平行四边形.
(3)?OAA1B1的面积=6×6=36.
点评:此题主要考查旋转的性质和平行四边形的判定以及面积的求法.

练习册系列答案
相关题目

 ,点P在线段AB上运动,点Q、R分别在线段BC、AC上,且使得四边形APQR是矩形.设AP的长为x,矩形APQR的面积为y,已知y是x的函数,其图象是过点(12,36)的抛物线的一部分(如图2所示).
,点P在线段AB上运动,点Q、R分别在线段BC、AC上,且使得四边形APQR是矩形.设AP的长为x,矩形APQR的面积为y,已知y是x的函数,其图象是过点(12,36)的抛物线的一部分(如图2所示).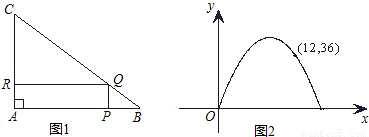
 (2009•株洲)如图是“北大西洋公约组织”标志的主体部分(平面图),它是由四个完全相同的四边形OABC拼成的.测得AB=BC,OA=OC,OA⊥OC,∠ABC=36°,则∠OAB的度数是( )
(2009•株洲)如图是“北大西洋公约组织”标志的主体部分(平面图),它是由四个完全相同的四边形OABC拼成的.测得AB=BC,OA=OC,OA⊥OC,∠ABC=36°,则∠OAB的度数是( )