��Ŀ����
����Ŀ���ڵ���������ABCD�У�AB=AC���ֱ�������AB��CA��ȡ��D��E������DE������E��EF��AB��ֱ��BC�ڵ�F��ֱ��BC��DE����ֱ�߽��ڵ�M��
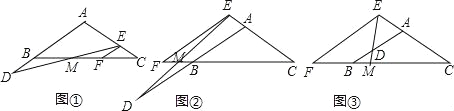
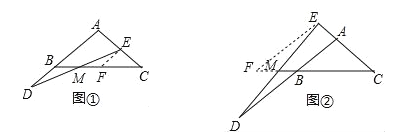
���룺��ͼ�٣���D�ڱ�AB�ӳ����ϣ���E�ڱ�AC�ϣ���BD=CE�����߶�BM��EM�Ĵ�С��ϵΪ ��
̽������ͼ�ڣ���D��E�ֱ��ڱ�AB��CA�ӳ����ϣ���BD=CE���ж��߶�DM��EM�Ĵ�С��ϵ��������֤����
��չ����ͼ�ۣ���D�ڱ�AB�ϣ���D�����A��B�غϣ�����E�ڱ�CA���ӳ����ϣ������������䣬��BD=1��CE=4��DM=0.7�����߶�DE�ij�Ϊ ��
���𰸡����룺DM=EM��̽����DM=EM����չ��2.1.
��������
�����������1�����ݵ��������ε����ʺ�ƽ���ߵ����ʵõ���D=��MEF��֤����BDM�ա�FEM���ɣ�
��2�����ݵ��������ε����ʺ�ƽ���ߵ����ʵõ���D=��MEF��֤����BDM�ա�FEM���ɣ�
��3�����ݵ��������ε����ʺ�ƽ���ߵ����ʵõ�EF=CE��BD��EF��![]() ���������ݼ��ɵõ����ۣ�
���������ݼ��ɵõ����ۣ�
�����������1�����룺DM=EM��
���ɣ���AB=AC��
���ABC=��C��
��EF��AD��
���EFC=��ABC��
���C=��EFC��
��EF=EC��
��BD=EC��
��DB=EF��
��EF��AB��
���D=��MEF��
�ڡ�BDM�͡�FEM�У�
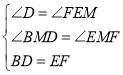 ��
��
���BDM�ա�FEM��
��DM=EM��
��2������DM=EM��
���ɣ���AB=AC��
���ABC=��C��
��EF��AB��
���EFC=��ABC��
���C=��EFC��
��EF=EC��
��BD=EC��
��DB=EF��
��EF��AB��
���D=��MEF��
�ڡ�BDM�͡�FEM�У�
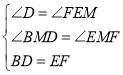 ��
��
���BDM�ա�FEM��
��DM=EM��
��3����EF��AB��
���F=��ABC��
��AB=AC��
���ABC=��C��
���F=��C��
��EF=CE=4��
��BD��EF��
��![]() ��
��
��![]() ��
��
��EM=2.8��
��DE=EM-DM=2.1��

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�