题目内容
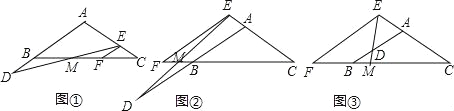
【题目】感知:如图①,在矩形ABCD中,点E是边BC的中点,将△ABE沿AE折叠,使点B落在矩形ABCD内部的点F处,延长AF交CD于点G,连结FC,易证∠GCF=∠GFC.
探究:将图①中的矩形ABCD改为平行四边形,其他条件不变,如图②,判断∠GCF=∠GFC是否仍然相等,并说明理由.
应用:如图②,若AB=5,BC=6,则△ADG的周长为 .

【答案】探究:∠GCF=∠GFC,理由见解析;应用:16.
【解析】
试题分析:探究:由ABCD及折叠可得∠B+∠ECG=∠AFE+∠ECG=∠AFE+∠EFG=180°,即∠ECG=∠EFG,再根据EB=EF=EC得∠EFC=ECF,从而可得∠GCF=∠GFC;
应用:由(1)中∠GCF=∠GFC得GF=GC,AF=AB,根据△ADG的周长AD+AF+GF+GD=AD+AB+GC+GD可得.
试题解析:探究:∠GCF=∠GFC,理由如下:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠ECG=180°,
又∵△AFE是由△ABE翻折得到,
∴∠AFE=∠B,EF=BE,
又∵∠AFE+∠EFG=180°,
∴∠ECG=∠EFG,
又∵点E是边BC的中点,
∴EC=BE,
∵EF=BE,
∴EC=EF,
∴∠ECF=∠EFC,
∴∠ECG-∠ECF=∠EFG-∠EFC,
∴∠GCF=∠GFC;
应用:∵△AFE是由△ABE翻折得到,
∴AF=AB=5,
由(1)知∠GCF=∠GFC,
∴GF=GC,
∴△ADG的周长AD+AF+GF+GD=AD+AB+GC+GD=AD+AB+CD=6+5+5=16

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目