题目内容
矩形ABCD的周长为16,点P是矩形边上任一点,则点P到对角线AC,BD的距离之和的最大值是
- A.8
- B.4
- C.

- D.

D
分析:先根据不等式a2+b2≥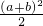 确定取得最大值时矩形的长与宽相等,此时求出矩形的对角线的长和面积,再根据点P与对角线的交点的连线把三角形分成两个小三角形的面积的和等于矩形面积的
确定取得最大值时矩形的长与宽相等,此时求出矩形的对角线的长和面积,再根据点P与对角线的交点的连线把三角形分成两个小三角形的面积的和等于矩形面积的 ,即可求出点P到两对角线点的距离的最大值.
,即可求出点P到两对角线点的距离的最大值.
解答: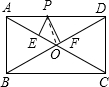 解:如图,设矩形的长为a,宽为b,
解:如图,设矩形的长为a,宽为b,
根据题意a+b=16÷2=8,
∵a2+b2≥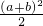 =32,
=32,
当且仅当a=b=4时,等号成立,
此时,对角线AC=BD= =
=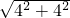 =4
=4 ,
,
因为矩形的四个三角形面积相等,均为 ×(4×4)=4,
×(4×4)=4,
设对角线交点为O,连接PO,
S△AOD=S△APO+S△DPO= AO•PE+
AO•PE+ OD•PF=
OD•PF= AO(PE+PF)=4,
AO(PE+PF)=4,
∵AO= AC=
AC= ×4
×4 =2
=2 ,
,
∴PE+PF=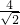 =2
=2 .
.
即点P到对角线AC,BD的距离之和的最大值是2 .
.
故选D.
点评:本题利用不等式得到当矩形的长与宽相等时,点P到对角线AC、BD的距离之和最大是解本题的关键,利用面积求解三角形的问题是常用的方法之一.
分析:先根据不等式a2+b2≥
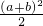 确定取得最大值时矩形的长与宽相等,此时求出矩形的对角线的长和面积,再根据点P与对角线的交点的连线把三角形分成两个小三角形的面积的和等于矩形面积的
确定取得最大值时矩形的长与宽相等,此时求出矩形的对角线的长和面积,再根据点P与对角线的交点的连线把三角形分成两个小三角形的面积的和等于矩形面积的 ,即可求出点P到两对角线点的距离的最大值.
,即可求出点P到两对角线点的距离的最大值.解答:
 解:如图,设矩形的长为a,宽为b,
解:如图,设矩形的长为a,宽为b,根据题意a+b=16÷2=8,
∵a2+b2≥
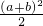 =32,
=32,当且仅当a=b=4时,等号成立,
此时,对角线AC=BD=
 =
=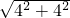 =4
=4 ,
,因为矩形的四个三角形面积相等,均为
 ×(4×4)=4,
×(4×4)=4,设对角线交点为O,连接PO,
S△AOD=S△APO+S△DPO=
 AO•PE+
AO•PE+ OD•PF=
OD•PF= AO(PE+PF)=4,
AO(PE+PF)=4,∵AO=
 AC=
AC= ×4
×4 =2
=2 ,
,∴PE+PF=
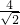 =2
=2 .
.即点P到对角线AC,BD的距离之和的最大值是2
 .
.故选D.
点评:本题利用不等式得到当矩形的长与宽相等时,点P到对角线AC、BD的距离之和最大是解本题的关键,利用面积求解三角形的问题是常用的方法之一.

练习册系列答案
相关题目
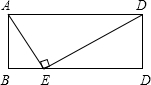 如图,在矩形ABCD中,E是BC上一点且∠AED=90°,∠BAE=30°,AE=4,则矩形ABCD的周长为( )
如图,在矩形ABCD中,E是BC上一点且∠AED=90°,∠BAE=30°,AE=4,则矩形ABCD的周长为( )A、8+2
| ||
B、16+2
| ||
C、8+4
| ||
D、16+4
|
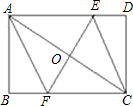 CE、EF,且EF与AC相交于点O.
CE、EF,且EF与AC相交于点O.