题目内容
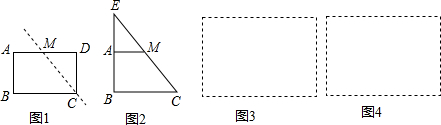
如图（1）的矩形纸片折叠，B、C两点恰好重合落在AD边上的点P处，如图（2），已知∠MPN=90°，PM=3，PN=4，那么矩形ABCD的周长为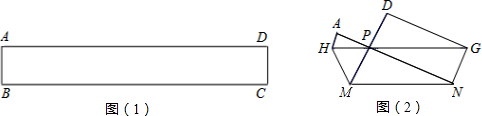
分析：根据勾股定理，得MN=5，进而可得出BC的长，根据直角三角形的面积公式的两种表示方法，可求出AB的长，根据矩形的周长=2（AB+BC）即可得出答案．
解答：解：由题意得，∠MPN=90°，PM=3cm，PN=4cm，
在RT△PMN中，MN2=PM2+PN2，
∴MN=5，BC=PM+PN+MN=3+4+5=12，
根据直角三角形的面积公式得，AB=
=
=2.4，
则矩形ABCD的周长=2（AB+BC）=28.8．
故答案为：28.8．
在RT△PMN中，MN2=PM2+PN2，
∴MN=5，BC=PM+PN+MN=3+4+5=12，
根据直角三角形的面积公式得，AB=
| PM•PN |
| MN |
| 12 |
| 5 |
则矩形ABCD的周长=2（AB+BC）=28.8．
故答案为：28.8．
点评：本题考查了翻折变换的知识，本题的解答利用了折叠的性质，折叠前后图形的形状和大小不变，对应边和对应角相等及勾股定理，另外要注意掌握直角三角形的面积的两种表示方法．
练习册系列答案
相关题目
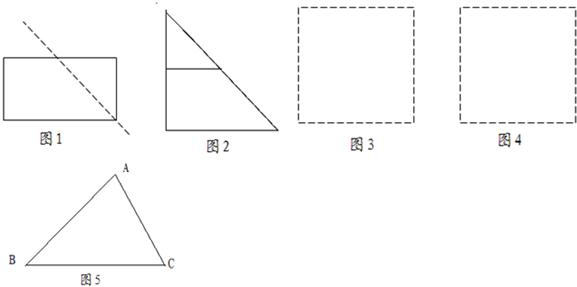
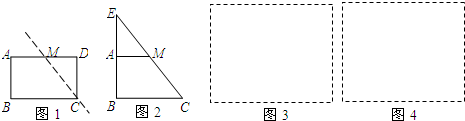
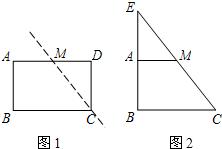剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分，其中M为AD的中点．用这两部分纸片可以拼成一些新图形，例如图2中的Rt△BCE就是拼成的一个图形．若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形，设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米，且a、b恰好是关于x的方程x2-（m-1）x+m+1=0的两个实数根，试求出原矩形纸片的面积．