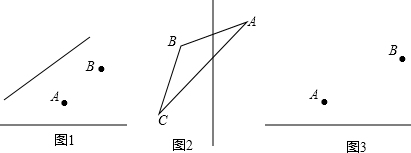
题目内容
作图题(保留作图过程,并做简要说明)
(1)如图1,作出△ABC关于直线l的对称图形;
(2)“西气东输”是造福子孙后代的创世纪工程.现有两条高速公路和A、B两个城镇(如图2),准备建立一个燃气中心站P,使中心站到两条公路距离相等,并且到两个城镇距离相等,请你画出中心站位置.
(3)河的一旁有两个村子A、B,要在河边建一水泵站引水到村里.一村民画了一张图(如图3),以直线l表示一条河,求作一点P,使P到A、B的距离和最短,作出P点,并用几何语言叙述你的理由.

解:(1)如图所示;
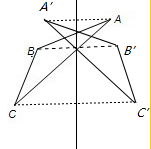
(2)如图所示;

(3)如图所示;

解:在直线l上任取一点Q,连接AQ、BQ,
∵A、C两点关于直线l轴对称,
∴AP=PC,AQ=CQ,CP+PB=BC,
又在△BCQ中,由三边关系定理,得BQ+CQ>BC,
即BQ+AQ>CP+BP,
∴BQ+CQ>AP+BP.
分析:(1)从三角形各顶点向直线引垂线,找三点关于直线的轴对称点,然后顺次连接就是所画的图形.
(2)到两条公路的距离相等,则要画两条公路的夹角的角平分线,到A,B两点的距离相等又要画线段AB的垂直平分线,两线的交点就是点P的位置.
(3)根据轴对称的性质,三角形三边关系定理判定线段的大小.
点评:此题主要考查了轴对称图形的性质、角平分线的性质及垂直平分线的性质和线段和最短的作法等知识,综合性较强,应熟练应用这些性质,解题的关键是根据“三角形两边之和大于第三边”,判断AP+BP最小.

(2)如图所示;

(3)如图所示;

解:在直线l上任取一点Q,连接AQ、BQ,
∵A、C两点关于直线l轴对称,

∴AP=PC,AQ=CQ,CP+PB=BC,
又在△BCQ中,由三边关系定理,得BQ+CQ>BC,
即BQ+AQ>CP+BP,
∴BQ+CQ>AP+BP.
分析:(1)从三角形各顶点向直线引垂线,找三点关于直线的轴对称点,然后顺次连接就是所画的图形.
(2)到两条公路的距离相等,则要画两条公路的夹角的角平分线,到A,B两点的距离相等又要画线段AB的垂直平分线,两线的交点就是点P的位置.
(3)根据轴对称的性质,三角形三边关系定理判定线段的大小.
点评:此题主要考查了轴对称图形的性质、角平分线的性质及垂直平分线的性质和线段和最短的作法等知识,综合性较强,应熟练应用这些性质,解题的关键是根据“三角形两边之和大于第三边”,判断AP+BP最小.

练习册系列答案
相关题目

 作图题:要求写出简单的作图过程,并保留作图痕迹,不要求证明.
作图题:要求写出简单的作图过程,并保留作图痕迹,不要求证明.