题目内容
【题目】如图，抛物线的表达式为y=ax2+4ax+4a-1（a≠0），它的图像的顶点为A，与x轴负半轴相交于点B、点C（点B在点C左侧），与y轴交于点D，连接AO交抛物线于点E，且S△AEC:S△CEO=1:3.
（1）求点A的坐标和抛物线表达式；
（2）在抛物线的对称轴上是否存在一点P，使得△BDP的内心也在对称轴上，若存在，求点P的坐标；若不存在，请说明理由；
（3）连接BD，点Q是y轴左侧抛物线上的一点，若以Q为圆心，
为半径的圆与直线BD相切，求点Q的坐标.
【答案】（1）抛物线表达式为y=x2+4x+3 ；（2）P（-2，-3）；（3）Q（-4，3）.
【解析】
（1）根据抛物线的对称轴易求得顶点坐标，再根据S△AEC:S△CEO=1:3，求得OE：OA=3:4，再证得△OFE∽△OMA，求得点E的坐标，从而求得答案；
（2）根据内心的定义知∠BPM=∠DPM，设点P（-2，b），根据三角函数的定义求得
，继而求得
的值，从而求得答案；
（3）设Q（m，m2+4m+3），分类讨论，①点Q在BD左上方抛物线上，②点Q在BD下方抛物线上，利用
的不同计算方法求得
的值，从而求得答案.
（1）由抛物线y=ax2+4ax+4a-1得对称轴为直线
，当时，
，
∴
，
∵S△AEC:S△CEO=1:3 ，
∴AE：OE=1:3 ，
∴OE：OA=3:4，
过点E作EF⊥x轴，垂足为点F，设对称轴与x轴交点为M，如图，
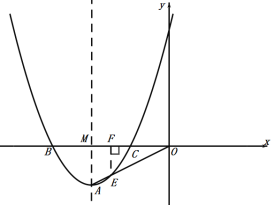
∵EF//AM ，
∴△OFE∽△OMA ，
∴ 
，
∴
，
∴
，
把点代入抛物线表达式y=ax2+4ax+4a-1得
，
解得：a=1，
∴抛物线表达式为：y=x2+4x+3 ；
（2）三角形的内心是三个角平分线的交点，
∴∠BPM=∠DPM，
过点D作DH⊥AM，垂足为点H，设点P（-2，b），
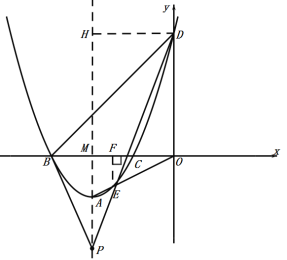
∵tan∠BPM=tan∠DPM ，
∴，
∴
，
∴
，
∴P（-2，-3），
（3）∵抛物线表达式为：y=x2+4x+3 ，
∴抛物线与
轴和
轴的交点坐标分别为：B(-3，0) ，C(-1，0) ，D(0，3) ，
∴
，
∴
设Q（m，m2+4m+3），
①点Q在BD左上方抛物线上，如图：作BG⊥x轴交BD于G，QF⊥x轴交于F，作QE⊥BD于E，
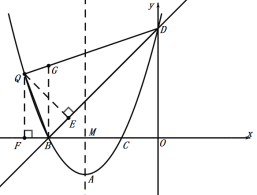
设直线QD的解析式为：
，
∵点Q的坐标为（m，m2+4m+3）代入得：
，
∴直线QD的解析式为：
，
当
时，
，
∴点G的坐标为；
，
∴
，
∵
，
∴
，
即：
，
解得：
或
(不合题意，舍去) ，
∴点
的坐标为：
②点Q在BD下方抛物线上，如图：QF⊥x轴交于F，交BD于G，作QE⊥BD于E，
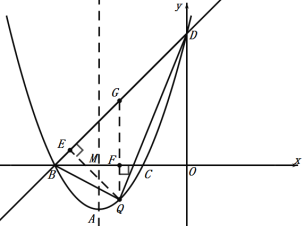
设直线BD的解析式为：，
将点B(-3，0)代入得：
，
∴直线BD的解析式为：
，
当
时，
，
∴点G的坐标为；
，
∴
，
∵，
∴
，
即：
，
∵
∴方程无解，
综上：点的坐标为：
）.
