题目内容
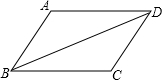 (2013•广州)已知四边形ABCD是平行四边形(如图),把△ABD沿对角线BD翻折180°得到△A′BD.
(2013•广州)已知四边形ABCD是平行四边形(如图),把△ABD沿对角线BD翻折180°得到△A′BD.(1)利用尺规作出△A′BD.(要求保留作图痕迹,不写作法);
(2)设DA′与BC交于点E,求证:△BA′E≌△DCE.
分析:(1)首先作∠A′BD=∠ABD,然后以B为圆心,AB长为半径画弧,交BA′于点A′,连接BA′,DA′,即可作出△A′BD.
(2)由四边形ABCD是平行四边形与折叠的性质,易证得:∠BA′D=∠C,A′B=CD,然后由AAS即可判定:△BA′E≌△DCE.
(2)由四边形ABCD是平行四边形与折叠的性质,易证得:∠BA′D=∠C,A′B=CD,然后由AAS即可判定:△BA′E≌△DCE.
解答: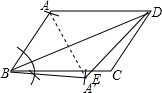 解:(1)如图:①作∠A′BD=∠ABD,
解:(1)如图:①作∠A′BD=∠ABD,
②以B为圆心,AB长为半径画弧,交BA′于点A′,
③连接BA′,DA′,
则△A′BD即为所求;
(2)∵四边形ABCD是平行四边形,
∴AB=CD,∠BAD=∠C,
由折叠的性质可得:∠BA′D=∠BAD,A′B=AB,
∴∠BA′D=∠C,A′B=CD,
在△BA′E和△DCE中,
,
∴△BA′E≌△DCE(AAS).
 解:(1)如图:①作∠A′BD=∠ABD,
解:(1)如图:①作∠A′BD=∠ABD,②以B为圆心,AB长为半径画弧,交BA′于点A′,
③连接BA′,DA′,
则△A′BD即为所求;
(2)∵四边形ABCD是平行四边形,
∴AB=CD,∠BAD=∠C,
由折叠的性质可得:∠BA′D=∠BAD,A′B=AB,
∴∠BA′D=∠C,A′B=CD,
在△BA′E和△DCE中,
|
∴△BA′E≌△DCE(AAS).
点评:此题考查了平行四边形的性质、折叠的性质以及全等三角形的判定与性质.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•广州)如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里.
(2013•广州)如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里.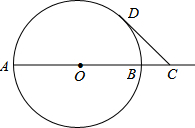 (2013•广州)已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.
(2013•广州)已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.