题目内容
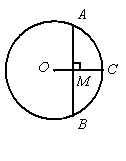
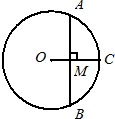如图，已知OC是⊙O的半径，弦AB=6，AB⊥OC，垂足为M，且CM=2．（1）连接AC，求∠CAM的正弦值；
（2）求OC的长．
分析：（1）由已知和垂径定理得，AM=3，再根据勾股定理求得AC，从而得出∠CAM的正弦值；
（2）连接OA，设OA=r，则OM=r-2，由勾股定理解得r即可．
（2）连接OA，设OA=r，则OM=r-2，由勾股定理解得r即可．
解答：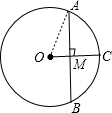
解：（1）∵OC是⊙O的半径，AB⊥OC，
∴AM=
AB=3．
在Rt△AMC中，CM=2，AM=3，
∴AC=
=
．
∴sin∠CAM=
=
；
（2）连接OA，设OA=r，则OM=r-2，
由勾股定理得（r-2）2+32=r2，
解得r=
．
解：（1）∵OC是⊙O的半径，AB⊥OC，∴AM=
| 1 |
| 2 |
在Rt△AMC中，CM=2，AM=3，
∴AC=
| 22+32 |
| 13 |
∴sin∠CAM=
| CM |
| AM |
2
| ||
| 13 |
（2）连接OA，设OA=r，则OM=r-2，
由勾股定理得（r-2）2+32=r2，
解得r=
| 13 |
| 4 |
点评：本题考查了垂径定理、勾股定理和锐角三角函数的定义．
练习册系列答案
相关题目
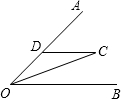
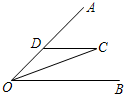14、如图，已知OC是∠AOB的平分线，DC∥OB，那么△DOC一定是
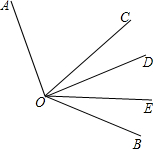如图．已知OC是∠AOB的平分线，OE是∠BOD的平分线，若∠COE=45°，求∠AOD的度数．
