题目内容
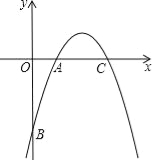
【题目】如图,已知二次函数y=﹣![]() x2+bx+c的图象经过(1,0),B(0,﹣6)两点,
x2+bx+c的图象经过(1,0),B(0,﹣6)两点,
(1)求这个二次函数解析式;
(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积;
(3)根据图象,写出函数值y为负数时,自变量x的取值范围;
(4)填空:要使该二次函数的图象与x轴只有一个交点,应该把图象沿y轴向下平移 个单位.
【答案】(1)、y=﹣![]() x2+
x2+![]() x﹣6;(2)、 S△ABC=
x﹣6;(2)、 S△ABC=![]() ×AC×OB=
×AC×OB=![]() ×11×6=33;(3)、x<1或x>12;(4)、
×11×6=33;(3)、x<1或x>12;(4)、![]()
【解析】
试题分析:(1)、利用待定系数法,将(1,0)、B(0,﹣6)代入y=﹣![]() x2+bc+c即可求出函数解析式;
x2+bc+c即可求出函数解析式;
(2)、根据解析式,求出C点坐标,再利用三角形面积公式即可求出△ABC的面积;(3)、根据抛物线与x轴的交点坐标,即可得出x的取值范围;(4)、求出抛物线的顶点纵坐标,即可根据平移知识得出答案.
试题解析:(1)、把(1,0)、B(0,﹣6)代入y=﹣![]() x2+bx+c,得:
x2+bx+c,得: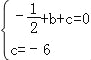 ,解得
,解得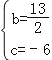 .
.
故这个二次函数的解析式为y=﹣![]() x2+
x2+![]() x﹣6;
x﹣6;
(2)、∵该抛物线对称轴为直线x=﹣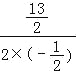 =
=![]() , ∴点C的坐标为(12,0),
, ∴点C的坐标为(12,0),
∴AC=OC﹣OA=12﹣1=11, ∴S△ABC=![]() ×AC×OB=
×AC×OB=![]() ×11×6=33;
×11×6=33;
(3)、由图可知,函数值y为负数时,自变量x的取值范围为x<1或x>12.
(4)、将(2)中所求x=![]() 代入解析式,即可得顶点纵坐标为﹣
代入解析式,即可得顶点纵坐标为﹣![]() ×(
×(![]() )2+
)2+![]() ×
×![]() ﹣6=
﹣6=![]() ,
,
可见把图象沿y轴向下平移![]() 个单位,则该二次函数的图象与x轴只有一个交点.
个单位,则该二次函数的图象与x轴只有一个交点.

练习册系列答案
相关题目