Question

当x=2时，抛物线y=ax²+bx+c取得最小值-1，并且抛物线与y轴交于点C（0，3），与x轴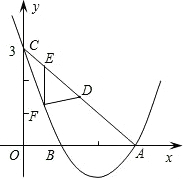交于点A、B．
（1）求该抛物线的关系式；
（2）若点M（x，y₁），N（x+1，y₂）都在该抛物线上，试比较y₁与y₂的大小；
（3）D是线段AC的中点，E为线段AC上一动点（A、C两端点除外），过点E作y轴的平行线EF与抛物线交于点F．问：是否存在△DEF与△AOC相似？若存在，求出点E的坐标；若不存在，则说明理由．

Answer 1

分析：（1）已知，当x=2时，抛物线的最小值为-1，因此抛物线的顶点坐标为（2，-1）；可用顶点式来设抛物线的解析式，然后将C的坐标代入即可求出抛物线的解析式．
（2）可先将M，N的坐标代入（1）的抛物线解析式中，可得出y₁、y₂的表达式．然后让y₁-y₂，然后看得出的结果中在x的不同取值范围下，y₁、y₂的大小关系．
（3）由于EF∥OC，那么∠FED=45°，因此要使三角形EFD与三角形COA相似，只有两种情况：
①当D为直角顶点时，∠EDF=90°，由于D是AC中点，而FD⊥AC，三角形AOC又是个等腰直角三角形，因此DF正好在∠COA的平分线上，即DF在直线y=x上，此时可先求出直线AC的函数关系式，然后联立抛物线的解析式求出F的坐标，由于E、F的横坐标相同，将F的横坐标代入AC所在的直线的解析式中即可求出E点的坐标．
②当F为直角顶点时，∠EFD=90°，那么DF与三角形AOC的中位线在同一直线上，即DF所在的直线的解析式为y=

3

2

，然后可根据①的方法求出E点的坐标．

解答：解：（1）由题意可设抛物线的关系式为
y=a（x-2）²-1
因为点C（0，3）在抛物线上
所以3=a（0-2）²-1，即a=1
所以，
抛物线的关系式为y=（x-2）²-1=x²-4x+3；

（2）∵点M（x，y₁），N（x+1，y₂）都在该抛物线上
∴y₁-y₂=（x²-4x+3）-[（x+1）²-4（x+1）+3]=3-2x
当3-2x＞0，即x＜

3

2

时，y₁＞y₂
当3-2x=0，即x=

3

2

时，y₁=y₂
当3-2x＜0，即x＞

3

2

时，y₁＜y₂

（3）令y=0，即x²-4x+3=0，
得点A（3，0），B（1，0），线段AC的中点为D（

3

2

，

3

2

）
直线AC的函数关系式为y=-x+3
因为△OAC是等腰直角三角形，
所以，要使△DEF与△AOC相似，△DEF也必须是等腰直角三角形．
由于EF∥OC，因此∠DEF=45°，
所以，在△DEF中只可能以点D、F为直角顶点．
①当F为直角顶点时，DF⊥EF，此时△DEF∽△ACO，DF所在直线为y=

3

2

由x²-4x+3=

3

2

，解得x=

4- 10

2

，x=

4+ 10

2

＞3（舍去）
将x=

4- 10

2

代入y=-x+3，
得点E（

4- 10

2

，

2+ 10

2

）
②当D为直角顶点时，DF⊥AC，此时△DEF∽△OAC，由于点D为线段AC的中点，
因此，DF所在直线过原点O，其关系式为y=x．
解x²-4x+3=x，得x=

5- 13

2

，x=

5+ 13

2

＞3（舍去）
将x=

5- 13

2

代入y=-x+3，
得点E（

5- 13

2

，

1+ 13

2

）．

点评：本题结合等腰三角形的相关知识考查了一次函数及二次函数的应用，要注意的是（3）中在不确定△EDF的直角顶点的情况下要分类进行讨论，不要漏解．