Question

【题目】如图，在 Rt△ABC中，∠ABC=90°，AB=CB，以AB为直径的⊙O交AC于点D，点E是AB边上一点（点E不与点A、B重合），DE的延长线交⊙O于点G，DF⊥DG，且交BC于点F．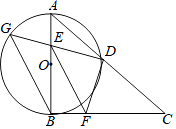

（1）求证：AE=BF．
（2）连接GB，EF，求证：GB∥EF．
（3）若AE=1，EB=3，求DG的长．

Answer 1

【答案】
（1）证明：连接BD，

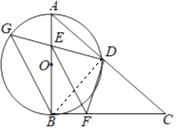
在Rt△ABC中，∠ABC=90°，AB=BC，

∴∠A=∠C=45°，

∵AB为圆O的直径，

∴∠ADB=90°，即BD⊥AC，

∴AD=DC=BD= AC，∠CBD=∠C=45°，

∴∠A=∠FBD，

∵DF⊥DG，

∴∠FDG=90°，

∴∠FDB+∠BDG=90°，

∵∠EDA+∠BDG=90°，

∴∠EDA=∠FDB，

在△AED和△BFD中，

，

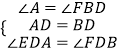∴△AED≌△BFD（ASA），

∴AE=BF

（2）证明：连接EF，BG，

∵△AED≌△BFD，

∴DE=DF，

∵∠EDF=90°，

∴△EDF是等腰直角三角形，

∴∠DEF=45°，

∵∠G=∠A=45°，

∴∠G=∠DEF，

∴GB∥EF

（3）解：∵AE=BF，AE=1，

∴BF=1，

在Rt△EBF中，∠EBF=90°，

∴根据勾股定理得：EF2=EB2+BF2，

∵EB=3，BF=1，

∴EF= = ，

∵△DEF为等腰直角三角形，∠EDF=90°，

∴cos∠DEF= ，

∵EF= ，

∴DE= × = ，

∵∠G=∠A，∠GEB=∠AED，

∴△GEB∽△AED，

∴ = ，即GEED=AEEB，

∴ GE=3，即GE= ，

则GD=GE+ED= ．

【解析】（1）连接BD，由△ABC为等腰直角三角形，可求出∠A与∠C的度数，根据AB为圆的直径，得到∠ADB为直角，即BD垂直于AC，利用直角三角形斜边上的中线等于斜边的一半，得到AD=DC=BD，进而得出∠A=∠FBD，再证明△AED≌△BFD，即可得证。
（2）连接EF，BG，由△AED≌△BFD，得到ED=FD，进而证得△DEF为等腰直角三角形，再证明∠G=∠DEF，即可得证；
（3）根据全等三角形对应边相等得到AE=BF=1，在Rt△BEF中，利用勾股定理求出EF的长，利用锐角三角形函数定义求出DE的长，利用两对角相等的三角形相似得到△GEB∽△AED，得对应边成比例，即可求出GE的长，由GE+ED求出GD的长即可。