题目内容
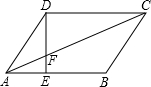如图，平行四边形ABCD中，E是AB上一点，DE与AC交于点F，且S△AEF=6cm2，S△DCF=54cm2，则S平行四边形ABCD=分析：根据平行四边形的性质可知△AEF∽△CDF，又这两三角形的面积知道，即可推出其相似比为1：3，则平行四边形的高为△AFE高的4倍，AB=3AE，那么平行四边形的面积是S△AEF的24倍．
解答：解：设S△AEF的高为h1，S△DCF的高为h2，平行四边形的高为h
∵平行四边形ABCD
∴△AEF∽△CDF
∵S△AEF=6cm2，S△DCF=54cm2∴AE：DC=AE：AB=1：3，h1：h2=1：3
∴AB=3AE
∵h=h1+h2∴h=4h1∵S△AEF=
AE•h1=6∴AE•h1=12
∴S平行四边形ABCD=AB•h=3AE•4h1=12AE•h1=144cm2
∵平行四边形ABCD
∴△AEF∽△CDF
∵S△AEF=6cm2，S△DCF=54cm2∴AE：DC=AE：AB=1：3，h1：h2=1：3
∴AB=3AE
∵h=h1+h2∴h=4h1∵S△AEF=
| 1 |
| 2 |
∴S平行四边形ABCD=AB•h=3AE•4h1=12AE•h1=144cm2
点评：利用平行四边形的性质和相似三角形的相似比求解，利用三角形相似，证明出所需线段的比值是解题的关键．
练习册系列答案
全能练考卷系列答案
相关题目
次方程x2-7x+12=0的两个根，且OA＞OB．
10、如图，平行四边形ABCD中，∠ABC的角平分线BE交AD于E点，AB=3，ED=1，则平行四边形ABCD的周长是
如图，平行四边形ABCD中，对角线AC和BD相交于点O，如果AC=12，BD=10，AB=m，那么m的取值范围是
如图，平行四边形ABCD的两条对角线AC、BD相交于点O，AB=5，AC=6，DB=8，则四边形ABCD是的周长为