题目内容

某种上屏每天的销售利润y（元）与销售单价x（元）之间满足关系：y=ax2+bx﹣75．其图象如图．
（1）销售单价为多少元时，该种商品每天的销售利润最大？最大利润为多少元？
（2）销售单价在什么范围时，该种商品每天的销售利润不低于16元？

（1）销售单价为10元时，该种商品每天的销售利润最大，最大利润为25元；（2）销售单价不少
于7元且不超过13元时，该种商品每天的销售利润不低于16元．

解析试题分析：（1）由已知，应用待定系数法，可得二次函数解析式，根据二次函数顶点坐标的性质，可得答案.
（2）根据函数值大于或等于16，可得不等式的解集，可得答案．
试题解析：解：（1）y=ax2+bx﹣75图象过点（5，0）、（7，16），
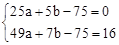∴，解得.
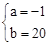∴y与x之间的函数关系为.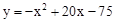
∵
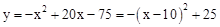
∴当x=10时，y最大=25，
答：销售单价为10元时，该种商品每天的销售利润最大，最大利润为25元.
（2）∵函数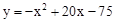图象的对称轴为直线x=10，
∴点（7，16）关于对称轴的对称点是（13，16）.
又∵函数y=﹣x2+20x﹣75图象开口向下，
∴当7≤x≤13时，y≥16．
答：销售单价不少于7元且不超过13元时，该种商品每天的销售利润不低于16元．
考点：1.二次函数的应用；2.曲线上点的坐标与方程的关系；3. 待定系数法的应用；4.二次函数的性质；5.数形结合思想的应用．

练习册系列答案
相关题目

二次函数图象的形状与y=3x2相同，且它的顶点坐标是，该解析式为             ；

如图①，在平面直角坐标系中，点A是抛物线y=x2在第一象限上的一个点，连结OA，过点A作AB⊥OA，交y轴于点B，设点A的横坐标为n．

【探究】：
（1）当n=1时，点B的纵坐标是　　；
（2）当n=2时，点B的纵坐标是　　；
（3）点B的纵坐标是　　（用含n的代数式表示）．
【应用】：
如图②，将△OAB绕着斜边OB的中点顺时针旋转180°，得到△BCO．
（1）求点C的坐标（用含n的代数式表示）；
（2）当点A在抛物线上运动时，点C也随之运动．当1≤n≤5时，线段OC扫过的图形的面积是　　．

如图，已知直线与x轴交于点A，与y轴交于点C，抛物线经过点A和点C，对称轴为直线l：，该抛物线与x轴的另一个交点为B．
（1）求此抛物线的解析式；
（2）点P在直线l上，求出使△PAC的周长最小的点P的坐标；
（3）点M在此抛物线上，点N在y轴上，以A、B、M、N为顶点的四边形能否为平行四边形？若能，直接写出所有满足要求的点M的坐标；若不能，请说明理由．

如图，抛物线y=ax2+x+c与x轴交于点A（4，0）、B（-1，0），与y轴交于点C，连接AC，点M是线段OA上的一个动点（不与点O、A重合），过点M作MN∥AC，交OC于点N，将△OMN沿直线MN折叠，点O的对应点O′落在第一象限内，设OM=t，△O′MN与梯形AMNC重合部分面积为S．
（1）求抛物线的解析式；
（2）①当点O′落在AC上时，请直接写出此时t的值；
②求S与t的函数关系式；
（3）在点M运动的过程中，请直接写出以O、B、C、O′为顶点的四边形分别是等腰梯形和平行四边形时所对应的t值．

已知抛物线y=x2﹣（k+2）x+和直线y=（k+1）x+（k+1）2．
（1）求证：无论k取何实数值，抛物线总与x轴有两个不同的交点；
（2）抛物线于x轴交于点A、B，直线与x轴交于点C，设A、B、C三点的横坐标分别是x1、x2、x3，求x1•x2•x3的最大值；
（3）如果抛物线与x轴的交点A、B在原点的右边，直线与x轴的交点C在原点的左边，又抛物线、直线分别交y轴于点D、E，直线AD交直线CE于点G（如图），且CA•GE=CG•AB，求抛物线的解析式．

如图，抛物线y=ax2+bx+c经过A（﹣3.0）、C（0，4），点B在抛物线上，CB∥x轴，且AB平分∠CAO．
（1）求抛物线的解析式；
（2）线段AB上有一动点P，过点P作y轴的平行线，交抛物线于点Q，求线段PQ的最大值；
（3）抛物线的对称轴上是否存在点M，使△ABM是以AB为直角边的直角三角形？如果存在，求出点M的坐标；如果不存在，说明理由．

已知抛物线y=x2+bx+c过点（-6,-2），与y轴交于点C，且对称轴与x轴交于点B（-2,0），顶点为A.
（1）求该抛物线的解析式和A点坐标；
（2）若点D是该抛物线上的一个动点，且使△DBC是以B为直角顶点BC为腰的等腰直角三角形，求点D坐标；
（3）若点M是第二象限内该抛物线上的一个动点，经过点M的直线MN与y轴交于点N，是否存在以O、M、N为顶点的三角形与△OMB全等？若存在，请求出直线MN的解析式；若不存在，请说明理由．

如图，抛物线的顶点为P（－2，2）与y轴交于点A（0，3），若平移该抛物线使其顶P沿直线移动到点，点A的对应点为，则抛物线上PA段扫过的区域（阴影部分）的面积为     .

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网