��Ŀ����
����Ŀ���ۺ���ʵ��������ת�е���ѧ
���ⱳ������һ���ۺ�ʵ������ϣ�ͬѧ������������Ϊ�����о����ƾ�����ת�е����⣺��֪����ABCD����A��B��C��D�䣬���Ǹ��ԶԽ��ߵĽ����غ��ڵ�O������AA�䣬CC�䣮��������ǽ���������⣺
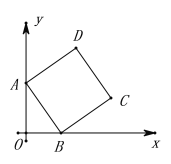
�۲췢�֣���1����ͼ1����A��B���AB����AA����CC���������ϵ��______��
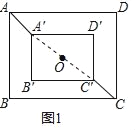
����̽������2����ͼ1�еľ���ABCD���ֲ���������A��B��C��D���Ƶ�O��ʱ����ת�ǶȦ���0�㣼����90�㣩����ͼ2���ھ���A��B��C��D����ת�Ĺ����У���1���еĽ��ۻ�����������������֤����������������˵�����ɣ�
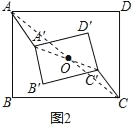
�������㣺��3����ͼ3���ڣ�2���������£�������A��B��C��D���Ƶ�O��ת��AA���A��D��ʱ����AB=6��BC=8��A��B��=3����AA��ij���

���𰸡�AA��=CC��
��������
��1������AC��A��C������������õ���A��A�䡢C�䡢C��ͬһ��ֱ���ϣ����ݾ��ε����ʵõ�OA=OC��OA��=OC�����õ��𰸣�
��2������AC��A��C����֤����A��OA�ա�C��OC������ȫ�������ε�����֤����
��3������AC����C��CE��AB������AB�����ӳ�����E���������ƶ���ε��������B��C�������ݹ��ɶ������㼴�ɣ�
��1��AA��=CC�䣬
�������£�����AC��A��C�䣬
�߾���ABCD����A��B��C��D�䣬��CAB=��C��A��B�䣬
��A��B����AB��
���A��A�䡢C�䡢C��ͬһ��ֱ���ϣ�
�ɾ��ε����ʿ�֪��OA=OC��OA��=OC�䣬
��AA��=CC�䣬
�ʴ�Ϊ��AA��=CC�䣻
��2����1���еĽ��ۻ�������AA��=CC�䣬
�������£�����AC��A��C������AC��A��C����������O��
����ת�����ʿ�֪����A��OA=��C��OC��
���ı���ABCD���ı���A��B��C��D�����Ǿ��Σ�
��OA=OC��OA��=OC�䣬
����A��OA����C��OC��
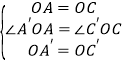 ��
��
���A��OA�ա�C��OC��
��AA��=CC�䣻
��3������AC����C��CE��AB������AB�����ӳ�����E��
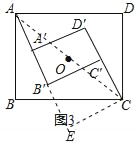
�߾���ABCD����A��B��C��D�䣬
��![]() ����
����![]() ��
��
��ã�B��C��=4��
�ߡ�EB��C=��B��C��C=��E=90�㣬
���ı���B��ECC��Ϊ���Σ�
��EC=B��C��=4��
��Rt��ABC��AC=![]() =10��
=10��
��Rt��AEC��AE=![]() =2
=2![]() ��
��
��AA��+B��E=2![]() ��3����AA��=CC��=B��E��
��3����AA��=CC��=B��E��
��AA��=![]() ��
��

 �����Ļ���������人������ϵ�д�
�����Ļ���������人������ϵ�д� ���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�
���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�