题目内容
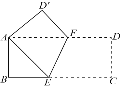
【题目】已知如图,在△ABC中,以AB、AC为直角边, 分别向外作等腰直角三角形ABE、ACF,连结EF,过点A作AD⊥BC,垂足为D,反向延长DA交EF于点M.
(1)用圆规比较EM与FM的大小.
(2)你能说明由(1)中所得结论的道理吗?

【答案】(1)EM=FM;(2)证明见解析.
【解析】
(1)直接用圆规比较两线段的大小;(2)作EH⊥AM,垂足为H,FK⊥AM,垂足为K.先说明Rt△EHA≌Rt△ADB, 得EH=AD,Rt△FKA≌Rt△ADC, 得FK=AD,得EH=FK,在Rt△EHK与Rt△FKM中,Rt△EHM≌Rt△FKM,得EM=FM.
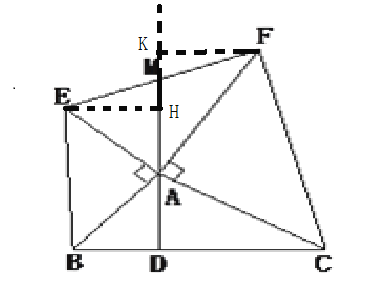
解:(1)EM=FM
(2)作EH⊥AM,垂足为H,FK⊥AM,垂足为K,则∠AHE=90,∠AKF=90,
因为,AD⊥BC,
所以,∠ADB=90,
所以,∠ABD+∠BAD=90,
又因为,△ABE是等腰直角三角形,
所以,AE=AB,∠BAE=90,
所以,∠EAH+∠BAD=90,
所以,∠EAH=∠ABD,
所以,Rt△EHA≌Rt△ADB(AAS),
所以,EH=AD,
同理:
Rt△FKA≌Rt△ADC, FK=AD,
所以EH=FK
在Rt△EHK与Rt△FKM中,
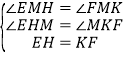
所以,Rt△EHM≌Rt△FKM(AAS)
得EM=FM.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目