题目内容
【题目】如图在□ABCD,∠ABC的平分线交AD于点E,延长BE交CD的延长线于F.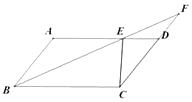
(1)若∠F=20°,求∠A的度数;
(2)若AB=5,BC=8,CE⊥AD,求□ABCD的面积;
【答案】
(1)
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=8,CD=AB=5,AB∥CD,
∴∠AEB=∠CBF,∠ABE=∠F=20°,
∵∠ABC的平分线交AD于点E,
∴∠ABE=∠CBF,
∴∠AEB=∠ABE=20°,
∴AE=AB,∠A=(180°-20°-20°)÷2=140°;
(2)
∵AE=AB=5,AD=BC=8,CD=AB=5,
∴DE=AD-AE=3,
∵CE⊥AD,
∴CE= ![]()
=4,
∴ABCD的面积=ADCE=8×4=32.
【解析】(1)由平行四边形的性质和已知条件得出∠AEB=∠CBF,∠ABE=∠F=20°,证出∠AEB=∠ABE=20°,由三角形内角和定理求出结果即可;(2)求出DE,由勾股定理求出CE,即可得出结果.
【考点精析】掌握三角形的内角和外角和勾股定理的概念是解答本题的根本,需要知道三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
相关题目