题目内容
(2002•济南)(1)在生活中需测量一些球的足球、篮球)的直径.某校研究性学习小组,通过实验发现下面的测量方法:如图,将球放在水平的桌面上,在阳光的斜射下,得到球的影子AB,设光线DA、CB分别与球相切于点E、F,则EF即为球的直径.若测得AB的长为41.5cm,∠ABC=37°.请你计算出球的直径(精确到1cm);(2)有一特殊材料制成的质量为30克的泥块,现把它切开为大小两块,将较大泥块放在一架不等臂天平的左盘中,称得质量为27克;又将较小泥块放在该天平的右盘中,称得质量为8克.若只考虑该天平的臂长不等,其他因素忽略不计,请你依据杠杆的平衡原理,求出较大泥块和较小泥块的质量.
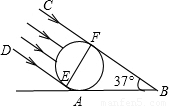
【答案】分析:(1)可通过构建直角三角形,将所求线段转换到直角三角形中进行计算.作AG⊥CB于G,那么四边形FEAG是个矩形,那么只要求出AG的值也就求出了小球的直径,直角三角形AGC中,有AB的长,有∠ABG的度数,因此可求出AG的长;
(2)本题中左边的物体的重量×左边天平臂长=右边的物体的重量×右边天平臂长,根据这个等量关系可将题中给出的大小泥块的在天平上测得的不同质量来列出方程组求出,大小泥块的质量.
解答: 解:(1)作AG⊥CB于G,
解:(1)作AG⊥CB于G,
∵DA,CB分别与圆相切于E,F
∴EF⊥FG,EF⊥EA
∴四边形AGFE是矩形
∴AG=EF
∴在Rt△ABG中,AB=41.5
∠ABG=37°
∴AG=AB•sin∠ABG=41.5×sin37°≈25
∴球的直径约为25cm;
(2)设较大泥块的质量为x克,则较小泥块的质量为(30-x)克,
若天平左,右臂长分别为acm,bcm由题意得:
 ,
,
两式相除得,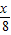 =
= ,
,
解得x1=18,x2=12.
经检验都是原方程的解,
根据题意x=12应该舍去,
当x=18时,30-x=12,
∴较大的泥块的质量为18克,较小的泥块的质量为12克.
点评:本题主要考查了切线的性质,解直角三角形以及方程组和分式方程的应用等知识点.
(2)本题中左边的物体的重量×左边天平臂长=右边的物体的重量×右边天平臂长,根据这个等量关系可将题中给出的大小泥块的在天平上测得的不同质量来列出方程组求出,大小泥块的质量.
解答:
 解:(1)作AG⊥CB于G,
解:(1)作AG⊥CB于G,∵DA,CB分别与圆相切于E,F
∴EF⊥FG,EF⊥EA
∴四边形AGFE是矩形
∴AG=EF
∴在Rt△ABG中,AB=41.5
∠ABG=37°
∴AG=AB•sin∠ABG=41.5×sin37°≈25
∴球的直径约为25cm;
(2)设较大泥块的质量为x克,则较小泥块的质量为(30-x)克,
若天平左,右臂长分别为acm,bcm由题意得:
 ,
,两式相除得,
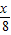 =
= ,
,解得x1=18,x2=12.
经检验都是原方程的解,
根据题意x=12应该舍去,
当x=18时,30-x=12,
∴较大的泥块的质量为18克,较小的泥块的质量为12克.
点评:本题主要考查了切线的性质,解直角三角形以及方程组和分式方程的应用等知识点.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
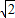 ,则这条抛物线解析式为( )
,则这条抛物线解析式为( )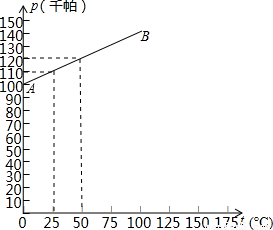

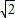 ,则这条抛物线解析式为( )
,则这条抛物线解析式为( )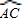 上一点,DE⊥AB于点H,交⊙O于点E,交AC于点F,P为ED的延长线上一点.
上一点,DE⊥AB于点H,交⊙O于点E,交AC于点F,P为ED的延长线上一点. 的什么位置时,才能使AD2=DE•DF.为什么?
的什么位置时,才能使AD2=DE•DF.为什么?