题目内容
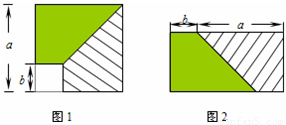
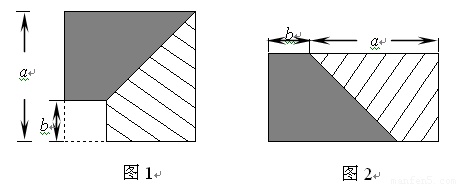
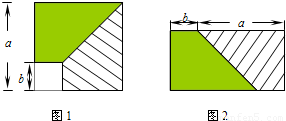
从边长为a的正方形内去掉一个边长为b的小正方形(如图1),然后将剩余部分剪拼成一个矩形(如图2),上述操作所能验证的等式是( )
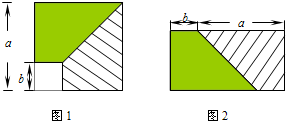

分析:分别求出从边长为a的正方形内去掉一个边长为b的小正方形后剩余部分的面积和拼成的矩形的面积,根据剩余部分的面积相等即可得出算式,即可选出选项.
解答:解:∵从边长为a的正方形内去掉一个边长为b的小正方形,剩余部分的面积是:a2-b2,
拼成的矩形的面积是:(a+b)(a-b),
∴根据剩余部分的面积相等得:a2-b2=(a+b)(a-b),
故选B.
拼成的矩形的面积是:(a+b)(a-b),
∴根据剩余部分的面积相等得:a2-b2=(a+b)(a-b),
故选B.
点评:本题考查了平方差公式的运用,解此题的关键是用算式表示图形的面积,用的数学思想是转化思想,即把实际问题转化成用数学式子表示出来.

练习册系列答案
相关题目
从边长为a的正方形内去掉一个边长为b的小正方形(如图1),然后将剩余部分剪拼成一个矩形(如图2),上述操作所能验证的等式是()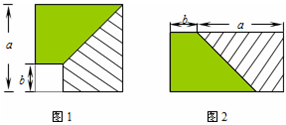
| A.(a-b)2=a2-2ab+b2 | B.a2-b2=(a+b)(a-b) |
| C.(a+b)2=a2+2ab+b2 | D.a2+ab=a(a+b) |