��Ŀ����
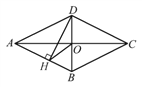
����Ŀ����һ��ֱ�����ǰ���ͼ�ٰڷţ��ܹ����ֵ���ֱ�����ǰ�ABC��б���뺬30��ǵ�ֱ�����ǰ�DEF�ij�ֱ�DZ�DE�غϣ�DF=8��
��1����P��BC�ϵ�һ�����㣬��PA=DFʱ�����ʱ��PAB�Ķ�����
��2����ͼ���еĵ���ֱ�����ǰ�ABC�Ƶ�B˳ʱ����ת30�㣬��C����BF�ϣ�AC��BD���ڵ�O������CD����ͼ�ڣ�
����֤��AD��BF��
����P��BC���е㣬����FP��������ֱ�����ǰ�ABC�Ƶ�B������ת������ת�Ǧ�= ʱ��FP����������ֵΪ ��ֱ��д���𰸼��ɣ���

���𰸡���1����PAB�Ķ���Ϊ15���75�㣻
��2���������������
��210�㣬16+4![]() ��
��
��������
�����������1������������Ǻ��������APH��Ȼ�������������㼴�ɣ�
��2��������AM��BC��DN��BC���õ�AM��DN���ڼ����AM��DN���õ�AM=DN������ƽ���ı���AMND�������жϳ�PF���ʱ����P����FB���ӳ����ϣ�����⼴�ɣ�
��ͼ1��
 D��
D��
�����������1����AH��BC��H����AH=![]() BC����DF=8����DEF=30�㣬��BC=DE=
BC����DF=8����DEF=30�㣬��BC=DE=![]() =8
=8![]() ��
��
��AH=4![]() ����PA=DF=8ʱ��sin��APH=
����PA=DF=8ʱ��sin��APH=![]() =
=![]() �����APH=60�㣬
�����APH=60�㣬
���ߡ�ABC=45�㣬��AP1H=60�㣬���BAP1=��AP1H����ABC=15�㣬
���ߡ�ACB=45�㣬��AP2H=60�㣬���CAP2=��AP2B����ACB=15�㣬
�ߡ�BAC=90�㣬���BAP2=90�㩁��CAP2=75�㣻���PAB�Ķ���Ϊ15���75�㣻
��2������ͼ2��AM��BC��DN��BC����Rt��ABC�У�AB=AC��BC=8![]() ��
��
��AM=![]() BC=
BC=![]() ��8
��8![]() =4
=4![]() ����Rt��BCF�У���F=60�㣬DF=8����DN=DF��sin��F=8��
����Rt��BCF�У���F=60�㣬DF=8����DN=DF��sin��F=8��![]() =4
=4![]() ��
��
��AM=DN����AM��DN�����ı���AMND��ƽ���ı��Σ���AD��BC��

����P��BC���е㣬��FP����������е�F��B��P��ͬһ��ֱ���ϣ�
������P��FB���ӳ����ϣ�
��BC����ת180�㣬
�ߡ�CDF=30�㣬
����ת�Ǧ�=210�㣬
��P��BC���е㣬BC=8![]() ��
��
��BP=4![]() ��
��
��BF=2DF=16��
��FP=16+4![]() ��
��
�ʴ�Ϊ210�㣬16+4![]() ��
��