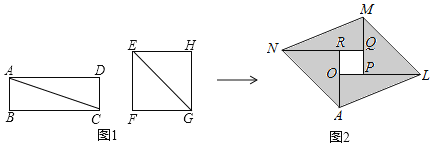题目内容
【题目】图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.
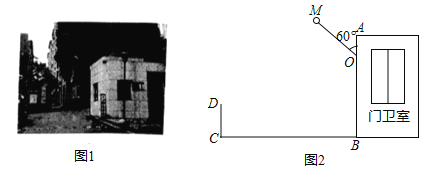
(1)求点M到地面的距离;
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:![]() 1.73,结果精确到0.01米)
1.73,结果精确到0.01米)
【答案】(1)3.9米;(2)货车能安全通过.
【解析】
(1)过M作MN⊥AB于N,交BA的延长线于N,在Rt△OMN中,求出ON的长,即可求得BN的长,即可求得点M到地面的距离;
(2)左边根据要求留0.65米的安全距离,即取CE=0.65,车宽EH=2.55,计算高GH的长即可,与3.5作比较,可得结论.
(1)如图,过M作MN⊥AB于N,交BA的延长线于N,
在Rt△OMN中,∠NOM=60°,OM=1.2,∴∠M=30°,
∴ON![]() OM=0.6,
OM=0.6,
∴NB=ON+OB=3.3+0.6=3.9,
即点M到地面的距离是3.9米;
(2)取CE=0.65,EH=2.55,∴HB=3.9﹣2.55﹣0.65=0.7,
过H作GH⊥BC,交OM于G,过O作OP⊥GH于P,
∵∠GOP=30°,∴tan30°![]() ,
,
∴GP![]() OP
OP![]() 0.404,
0.404,
∴GH=3.3+0.404=3.704≈3.70>3.5,
∴货车能安全通过.

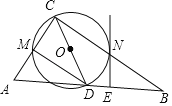
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.

(1)该三角形的外接圆的半径长等于 ;
(2)用直尺和圆规作出该三角形的内切圆(不写作法,保留作图痕迹),并求出该三角形内切圆的半径长.
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为在40元的基础上上涨x(x>0),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润W(元),并把结果填写在表格中:
销售单价(元) | 40+x |
销售量y(件) |
|
销售玩具获得利润W(元) |
|
(2)在(1)问条件下,若商场获得10000元销售利润,则该玩具销售单价应定为多少元?
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?