题目内容
 已知:关于x的一元二次方程kx2+2x+2-k=0.
已知:关于x的一元二次方程kx2+2x+2-k=0.(1)若原方程有实数根,求k的取值范围;
(2)设原方程的两个实数根分别为x1,x2.
①当k取哪些整数时,x1,x2均为整数;
②利用图象,估算关于k的方程x1+x2+k-1=0的解.
分析:(1)根据根的判别式列出不等式,变形为完全平方式知△≥0,二次项系数≠0,得出k的取值范围.
(2)利用求根公式求出一元二次方程的两根,两根均为整数得出k的整数值,把两根代入得出关于k的方程,转化成一次函数和反比例函数作出图象,找出交点坐标.
(2)利用求根公式求出一元二次方程的两根,两根均为整数得出k的整数值,把两根代入得出关于k的方程,转化成一次函数和反比例函数作出图象,找出交点坐标.
解答:解:(1)∵一元二次方程kx2+2x+2-k=0有实数根,
∴
,
∴
,
∴当k≠0时,一元二次方程kx2+2x+2-k=0有实数根.
(2)①由求根公式,得x=
.
∴x1=
=1-
,x2=-1,
要使x1,x2均为整数,
必为整数,
所以,当k取±1或±2时,x1,x2均为整数;
②将x1=1-
,x2=-1代入方程x1+x2+k-1=0中,得
=k-1.
设y1=
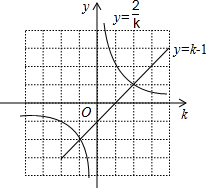
,y2=k-1,并在同一平面直角坐标系中分别画出y1=
与y2=k-1的图象(如图所示).
由图象可得,关于k的方程x1+x2+k-1=0的解为k1=-1,k2=2.
∴
|
∴
|
∴当k≠0时,一元二次方程kx2+2x+2-k=0有实数根.
(2)①由求根公式,得x=
| -1±(k-1) |
| k |
∴x1=
| k-2 |
| k |
| 2 |
| k |
要使x1,x2均为整数,
| 2 |
| k |
所以,当k取±1或±2时,x1,x2均为整数;
②将x1=1-
| 2 |
| k |
| 2 |
| k |
设y1=
| 2 |
| k |
| 2 |
| k |
由图象可得,关于k的方程x1+x2+k-1=0的解为k1=-1,k2=2.

点评:考查一元二次方程根的判别式及求根公式,一次函数和二次函数的作图.

练习册系列答案
相关题目