题目内容
【题目】实数k取何值时,一元二次方程x2-(2k-3)x+2k-4=0:
(1)有两个正根;
(2)有两个异号根,并且正根的绝对值较大;
(3)一根大于3,一根小于3.
【答案】(1)见解析。(2)见解析,(3)见解析。
【解析】
根据一元二次方程根与系数的关系,即韦达定理进行作答.(1)有两个正根时,x1>0,x2>0,即x1+x2![]() ,x1x2
,x1x2![]() .由此得到k的取值.(2)有两个异号根,并且正根的绝对值较大,即x1>0,x2<0且|x1|>|x2|.即x1+x2
.由此得到k的取值.(2)有两个异号根,并且正根的绝对值较大,即x1>0,x2<0且|x1|>|x2|.即x1+x2![]() ,x1x2
,x1x2![]() .由此得到k的取值.(3)一根大于3,一根小于3时,即x1>3,x2<3. 则k应满足条件:(x1-3)(x2-3)<0,即x1x2-3(x1+x2)+9<0. 由此得到k的取值.
.由此得到k的取值.(3)一根大于3,一根小于3时,即x1>3,x2<3. 则k应满足条件:(x1-3)(x2-3)<0,即x1x2-3(x1+x2)+9<0. 由此得到k的取值.
解:∵Δ=[-(2k-3)]2-4(2k-4)=4k2-20k+25=(2k-5)2≥0,∴k取任何实数,方程都有两个实数根.设该方程的两根为x1,x2,则由韦达定理,得x1+x2=2k-3,x1x2=2k-4.
(1)若使x1>0,x2>0,则k应满足条件:![]() 解得
解得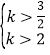 ,∴当k>2时,方程有两个正根.
,∴当k>2时,方程有两个正根.
(2)若使x1>0,x2<0且|x1|>|x2|,则k应满足条件:![]() 解得
解得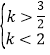 ,∴当
,∴当![]() <k<2时,两根异号,且正根的绝对值较大.
<k<2时,两根异号,且正根的绝对值较大.
(3)若使x1>3,x2<3,则k应满足条件:(x1-3)(x2-3)<0,即x1x2-3(x1+x2)+9<0.∴2k-4-3(2k-3)+9<0,k>![]() .∴当k>
.∴当k>![]() 时,方程一根大于3,另一根小于3.
时,方程一根大于3,另一根小于3.

【题目】我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 | 6.7 | m | 3.41 | 90% | n |
八年级 | 7.1 | 7.5 | 1.69 | 80% | 10% |
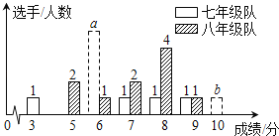
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.