题目内容
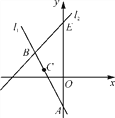
【题目】如图,直线l1在平面直角坐标系中,直线l1与y轴交于点A,点B(-3,3)也在直线l1上,将点B先向右平移1个单位长度,再向下平移2个单位长度得到点C,点C恰好也在直线l1上.
(1)求点C的坐标和直线l1的解析式;
(2)已知直线l2:y=x+b经过点B,与y轴交于点E,求△ABE的面积.
【答案】(1)y=-2x-3.(2) 13.5
【解析】(1)根据平移的性质得到点C的坐标;把点B、C的坐标代入直线方程y=kx+b(k≠0)来求该直线方程;
(2)根据点B的坐标求得直线l2的解析式,据此求得相关线段的长度,并利用三角形的面积公式进行解答.
解:(1)由题意得:点C的坐标为(-2,1).
设直线l1的解析式为y=kx+c,
∵点B,C在直线l1上,
∴![]() ,
,
解得![]() ,
,
∴直线l1的解析式为y=-2x-3.
(2)把点B的坐标代入y=x+b,
得3=-3+b,
解得b=6,
∴y=x+6,
∴点E的坐标为(0,6),
∵直线y=-2x-3与y轴交于A点,
∴A的坐标为(0,-3),
∴AE=6+3=9,
∵B(-3,3),
∴S△ABE=![]() ×9×|-3|=13.5.
×9×|-3|=13.5.

练习册系列答案
相关题目


