ĢāÄæÄŚČŻ
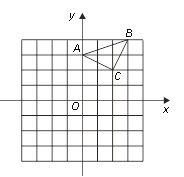
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Å×ĪļĻßy=ax2+![]() x+c¹żµćA£Ø0£¬4£©ŗĶC£Ø8£¬0£©£¬P£Øt£¬0£©ŹĒxÖįÕż°ėÖįÉĻµÄŅ»øö¶Æµć£¬MŹĒĻ߶ĪAPµÄÖŠµć£¬½«Ļ߶ĪMPČʵćPĖ³Ź±ÕėŠż×Ŗ90”ćµĆĻ߶ĪPB£®¹żµćB×÷xÖįµÄ“¹Ļß”¢¹żµćA×÷yÖįµÄ“¹Ļߣ¬Į½Ö±ĻßĻą½»ÓŚµćD£®
x+c¹żµćA£Ø0£¬4£©ŗĶC£Ø8£¬0£©£¬P£Øt£¬0£©ŹĒxÖįÕż°ėÖįÉĻµÄŅ»øö¶Æµć£¬MŹĒĻ߶ĪAPµÄÖŠµć£¬½«Ļ߶ĪMPČʵćPĖ³Ź±ÕėŠż×Ŗ90”ćµĆĻ߶ĪPB£®¹żµćB×÷xÖįµÄ“¹Ļß”¢¹żµćA×÷yÖįµÄ“¹Ļߣ¬Į½Ö±ĻßĻą½»ÓŚµćD£®
£Ø1£©Ēó“ĖÅ×ĪļĻߵĶŌ³ĘÖį£»
£Ø2£©µ±tĪŖŗĪÖµŹ±£¬µćDĀäŌŚÅ×ĪļĻßÉĻ£æ
£Ø3£©ŹĒ·ń“ęŌŚt£¬Ź¹µĆŅŌA”¢B”¢DĪŖ¶„µćµÄČż½ĒŠĪÓė”÷PEBĻąĖĘ£æČō“ęŌŚ£¬Ēó“ĖŹ±tµÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®

”¾“š°ø”æ£Ø1£©¶Ō³ĘÖįĪŖ£ŗx=![]() £»£Ø2£©µ±t=3Ź±£¬µćDĀäŌŚÅ×ĪļĻßÉĻ£»£Ø3£©µ±t=©2+2
£»£Ø2£©µ±t=3Ź±£¬µćDĀäŌŚÅ×ĪļĻßÉĻ£»£Ø3£©µ±t=©2+2![]() ”¢t=8+4
”¢t=8+4![]() Ź±£¬ŅŌA”¢B”¢DĪŖ¶„µćµÄČż½ĒŠĪÓė”÷PEBĻąĖĘ£®
Ź±£¬ŅŌA”¢B”¢DĪŖ¶„µćµÄČż½ĒŠĪÓė”÷PEBĻąĖĘ£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©øł¾ŻĢāŅāĄūÓĆ“ż¶ØĻµŹż·ØĒó³öŗÆŹż½āĪöŹ½£¬“Ó¶ųµĆµ½¶Ō³ĘÖį£»£Ø2£©øł¾ŻĢāŅāµĆ³öµćMµÄ×ų±ź£¬øł¾ŻŠż×ŖµÄŠŌÖŹµĆ³öµćEŗĶµćBµÄ×ų±ź£¬“Ó¶ųµĆµ½µćDµÄ×ų±ź£¬Č»ŗóĒó³ötµÄÖµ£»£Ø3£©·Ö0£¼t£¼8ŗĶt£¾8Į½ÖÖĒéæö£¬ĆæÖÖĒéæö·ÖĮ½ÖÖĒéæö½ųŠŠĢÖĀŪ¼ĘĖć£¬µĆ³ötµÄÖµ£®
ŹŌĢā½āĪö£ŗ£Ø1£©ÓÉĢāµĆ£¬ £¬½āµĆ
£¬½āµĆ £®
£®
![]() Å×ĪļĻߵĽāĪöŹ½ĪŖ£ŗ
Å×ĪļĻߵĽāĪöŹ½ĪŖ£ŗ ![]() £¬ĖüµÄ¶Ō³ĘÖįĪŖ£ŗ
£¬ĖüµÄ¶Ō³ĘÖįĪŖ£ŗ ![]()
£Ø2£©ÓÉĢāŅāµĆ£ŗ ![]() £¬
£¬ ![]() £®
£®
![]() ŹĒ
ŹĒ![]() ČʵćPĖ³Ź±ÕėŠż×Ŗ90”ć¶ųµĆ£¬
ČʵćPĖ³Ź±ÕėŠż×Ŗ90”ć¶ųµĆ£¬ ![]()
![]() £¬
£¬ ![]() £®“Ó¶ųÓŠ
£®“Ó¶ųÓŠ![]() £®
£®
¼ŁÉč![]() ŌŚÅ×ĪļĻßÉĻ£¬ÓŠ
ŌŚÅ×ĪļĻßÉĻ£¬ÓŠ![]() £¬ ½āµĆ
£¬ ½āµĆ![]()
”ß![]() £¬¼“µ±
£¬¼“µ±![]() Ź±£¬µćDĀäŌŚÅ×ĪļĻßÉĻ£®
Ź±£¬µćDĀäŌŚÅ×ĪļĻßÉĻ£®
£Ø3£©¢Łµ±![]() Ź±£¬ČēĶ¼£¬
Ź±£¬ČēĶ¼£¬

![]() £¬
£¬
£Ø1£©Čō”÷![]() ”×”÷ADB£¬“ĖŹ±
”×”÷ADB£¬“ĖŹ±![]() £¬ÓŠ£ŗ
£¬ÓŠ£ŗ ![]() £¬ £¬¼“
£¬ £¬¼“ £¬
£¬
»Æ¼ņµĆ![]() £¬“ĖŹ±
£¬“ĖŹ±![]() ĪŽ½ā”£
ĪŽ½ā”£
Čō”÷![]() ”×”÷ADB£¬ “ĖŹ±
”×”÷ADB£¬ “ĖŹ±![]() £¬ÓŠ£ŗ
£¬ÓŠ£ŗ ![]() £¬ £¬¼“
£¬ £¬¼“ £¬
£¬
»Æ¼ņµĆ£ŗ ![]() £¬¹ŲÓŚ
£¬¹ŲÓŚ![]() µÄŅ»ŌŖ¶ž“Ī·½³ĢµÄÅŠ±šŹ½
µÄŅ»ŌŖ¶ž“Ī·½³ĢµÄÅŠ±šŹ½![]() £¬
£¬
ÓÉĒóøł¹«Ź½µĆ£ŗ![]()
![]() £¬
£¬ ![]() ”£
ӣ
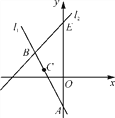
¢Śµ±![]() Ź±£¬ČēĶ¼¢Ś£¬Čō”÷POA”×”÷ADB
Ź±£¬ČēĶ¼¢Ś£¬Čō”÷POA”×”÷ADB![]()
£Ø1£©Čō”÷![]() ”×”÷ADB£¬“ĖŹ±
”×”÷ADB£¬“ĖŹ±![]() £¬ÓŠ£ŗ
£¬ÓŠ£ŗ
![]() £¬¼“
£¬¼“ £¬»Æ¼ņµĆ
£¬»Æ¼ņµĆ![]() £¬½āµĆ
£¬½āµĆ![]() £ØøŗøłÉįČ„£©”£
£ØøŗøłÉįČ„£©”£
£Ø2£©Čō”÷![]() ”×”÷ADB£¬Ķ¬ĄķµĆ“ĖŹ±
”×”÷ADB£¬Ķ¬ĄķµĆ“ĖŹ±![]() ĪŽ½ā”£
ĪŽ½ā”£
×ŪŗĻÉĻŹö£ŗµ±![]() ”¢
”¢![]() Ź±£¬ŅŌA”¢B”¢DĪŖ¶„µćµÄČż½ĒŠĪÓė”÷PEBĻąĖĘ”£
Ź±£¬ŅŌA”¢B”¢DĪŖ¶„µćµÄČż½ĒŠĪÓė”÷PEBĻąĖĘ”£