Question

将三角形纸片（△ABC）按如图所示的方式折叠，使点B落在边AC上，记为点B'，折痕为EF．已知AB=AC=2，cosC=

3

4

，若以点B'、F、C为顶点的三角形与△ABC相似，那么BF的长度是______．

Answer 1

作AH⊥BC，垂足为H，在Rt△ACH中，CH=AC•cosC=

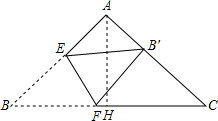
3

2

，
∵AB=AC，∴BC=2CH=3，
∵以点B'、F、C为顶点的三角形与△ABC相似，
∴B′F=B′C，∴FB′∥AB，
∴∠B′FE=∠FEB，
由折叠的性质可知，∠B′FE=∠BFE，∠FEB=∠FEB′，
∴四边形BFB′E为菱形，
设BF=x，则B′F=B′C=B′E=x，AB′=2-x，
∵B′E∥BC，∴△AEB′∽△ABC，
∴

B′E

BC

=

AB′

AC

，即

x

3

=

2-x

2

，解得x=

6

5

．
故答案为：

6

5

．