题目内容
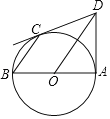
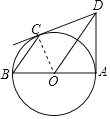
【题目】已知:如图,AB是⊙O的直径,直线DC,DA分别切⊙O于点C,点A,连结BC,OD.
(1)求证:BC∥OD.
(2)若∠ODC=36°,AB=6,求出![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() 的长=
的长=![]() .
.
【解析】
(1)连接OC,根据切线长定理得到CD=AD,根据全等三角形的性质得到∠AOD=∠COD,根据圆周角定理得到∠B=∠AOD,于是得到结论;
(2)根据切线长定理得到∠ADC=2∠CDO=72°,根据四边形的内角和得到∠AOC=180°﹣∠ADC=108°,求得∠BOC=72°,根据弧长公式即可得到结论.
解:(1)连接OC,
∵直线DC,DA分别切⊙O于点C,
∴CD=AD,
在△ADO与△CDO中,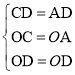 ,
,
∴△ADO≌△CDO(SSS),
∴∠AOD=∠COD,
∴∠AOD=![]() AOC,
AOC,
∵∠B=![]() AOC,
AOC,
∴∠B=∠AOD,
∴BC∥OD;
(2)∵∠ODC=36°,直线DC,DA分别切⊙O于点C,点A,
∴∠ADC=2∠CDO=72°,
∴∠AOC=180°﹣∠ADC=108°,
∴∠BOC=72°,
∵AB=6,
∴OB=3,
∴![]() 的长=
的长=![]() =
=![]() .
.

练习册系列答案
相关题目
【题目】学校李老师布置了两道解方程的作业题:
选用合适的方法解方程:
(1)x(x+1)=2x;(2)(x+1)(x﹣3)=7
以下是王萌同学的作业:
解:(1)移项,得x(x+1)﹣2x=0 分解因式得,x(x+1﹣2)=0 所以,x=0,或x﹣1=0 所以,x1=0,x2=1 | (2)变形得,(x+1)(x﹣3)=1×7 所以,x+1=7,x﹣3=1 解得,x1=6,x2=4 |
请你帮王萌检查他的作业是否正确,把不正确的改正过来.