Question

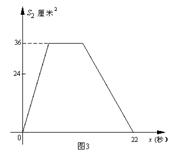
如图1，在矩形ABCD中，AB＝12厘米，BC=6厘米，点P从A点出发，沿A →B→C→D路线运动，到D点停止；点Q从D点出发，沿D →C →B →A运动，到A点停止．若点P，点Q同时出发，点P的速度为每秒1厘米，点Q的速度为每秒2厘米，a秒时点P，点Q同时改变速度，点P的速度变为每秒b厘米，点Q的速度变为每秒c厘米．如图2是描述点P出发x秒后△APD的面积S1（）与x(秒)的函数关系的图象．图3是描述点Q出发x秒后△AQD的面积S2（）与x(秒)的函数关系图象．根据图象：

（1）求a、b、c的值；

（2）设点P离开点A的路程为y1(厘米)，点Q到点A还需要走的路程为y2(厘米)，请分别写出改变速度后y1、y2与出发后的运动时间x(秒)的函数关系式，并求出P与Q相遇时x的值．

 

Answer 1

【答案】

 

（1）8   2     1

（2）出发１０秒后，Ｐ与Ｑ相遇

【解析】（1）解：（１）观察图象，得

　　　　　

　　　　　　……………２分

　　　　　　

　（２）依题意得，

　　　　　

　　　　依题意，当时，Ｐ与Ｑ相遇，即

　　　　　解得，

　　　　所以，出发１０秒后，Ｐ与Ｑ相遇．