题目内容
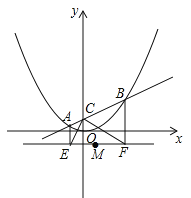
【题目】已知,如图①,在ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4),连接PQ,MQ,MC,解答下列问题:
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与x之间的函数关系式;
(3)是否存在某一时刻t,使S△QMC:S四边形ABQP=1:4?若存在,求出t的值;若不存在,请说明理由.
(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() (0<t<4);(3)t=2;(4)
(0<t<4);(3)t=2;(4)![]() .
.
【解析】
试题分析:(1)根据勾股定理求出AC,根据PQ∥AB,得出![]() ,
,![]() ,求解即可;
,求解即可;
(2)过点P作PD⊥BC于D,根据△CPD∽△CBA,得出![]() ,求出PD=
,求出PD=![]() ,再根据S△QMC=S△QPC,得出y=S△QMC=
,再根据S△QMC=S△QPC,得出y=S△QMC=![]() QCPD,再代入计算即可;
QCPD,再代入计算即可;
(3)根据S△QMC:S四边形ABQP=1:4,得出S△QPC:S△ABC=1:5,代入得出(![]() ):6=1:5,再计算即可;
):6=1:5,再计算即可;
(4)根据PQ⊥MQ得出△PDQ∽△MQP,得出![]() =MPDQ,根据勾股定理得出
=MPDQ,根据勾股定理得出![]() =MPDQ,再分别代入得出
=MPDQ,再分别代入得出![]() ,求出t即可.
,求出t即可.
试题解析:(1)在Rt△ABC中,AC=![]() =4,由平移的性质得MN∥AB,∵PQ∥MN,∴PQ∥AB,∴
=4,由平移的性质得MN∥AB,∵PQ∥MN,∴PQ∥AB,∴![]() ,∴
,∴![]() ,解得
,解得![]() ;
;
(2)过点P作PD⊥BC于D,∵△CPD∽△CBA,∴![]() ,∴
,∴![]() ,∴PD=
,∴PD=![]() ,∵PD∥BC,∴S△QMC=S△QPC,∴
,∵PD∥BC,∴S△QMC=S△QPC,∴![]() ,即
,即![]() (0<t<4);
(0<t<4);
(3)∵S△QMC:S四边形ABQP=1:4,∴S△QPC:S四边形ABQP=1:4,∴S△QPC:S△ABC=1:5,![]() ):6=1:5,整理得:
):6=1:5,整理得:![]() ,解得
,解得![]() ;
;
(4)若PQ⊥MQ,则∠PQM=∠PDQ,∵∠MPQ=∠PQD,∴△PDQ∽△MQP,∴![]() ,∴
,∴![]() =MPDQ,∴
=MPDQ,∴![]() =MPDQ,∵CD=
=MPDQ,∵CD=![]() ,∴DQ=CD﹣CQ=
,∴DQ=CD﹣CQ=![]() =
=![]() ,∴
,∴![]() ,∴整理得
,∴整理得![]() ,解得
,解得![]() (舍去),
(舍去),![]() ,∴
,∴![]() 时,PQ⊥MQ.
时,PQ⊥MQ.

【题目】某校七年级实行小组合作学习,为了解学生课堂发言情况,随机抽取该年级部分学生,对他们每天在课堂中发言的次数进行调查和统计,统计表如下,并绘制了两幅不完整的统计图(如图所示).已知A、B两组发言人数直方图高度比为1∶5,请结合图中相关的数据回答下列问题:
发言次数n | |
A | 0≤n<5 |
B | 5≤n<10 |
C | 10≤n<15 |
D | 15≤n<20 |
E | 20≤n<25 |
F | 25≤n<30 |

(1)A组的人数是多少?本次调查的样本容量是多少?
(2)求出C组的人数,并补全直方图;
(3)该校七年级共有250人.请估计全年级每天在课堂中发言次数不少于15次的人数是多少?