题目内容
 (2013•成都)如图,点B在线段AC上,点D,E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
(2013•成都)如图,点B在线段AC上,点D,E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.(1)求证:AC=AD+CE;
(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q;
(i)当点P与A,B两点不重合时,求
| DP | PQ |
(ii)当点P从A点运动到AC的中点时,求线段DQ的中点所经过的路径(线段)长.(直接写出结果,不必写出解答过程)
分析:(1)根据同角的余角相等求出∠1=∠E,再利用“角角边”证明△ABD和△CEB全等,根据全等三角形对应边相等可得AB=CE,然后根据AC=AB+BC整理即可得证;
(2)(i)过点Q作QF⊥BC于F,根据△BFQ和△BCE相似可得
=
,然后求出QF=
BF,再根据△ADP和△FPQ相似可得
=
,然后整理得到(AP-BF)(5-AP)=0,从而求出AP=BF,最后利用相似三角形对应边成比例可得
=
,从而得解;
(ii)判断出DQ的中点的路径为△BDQ的中位线MN.求出QF、BF的长度,利用勾股定理求出BQ的长度,再根据中位线性质求出MN的长度,即所求之路径长.
(2)(i)过点Q作QF⊥BC于F,根据△BFQ和△BCE相似可得
| BF |
| BC |
| QF |
| CE |
| 5 |
| 3 |
| AD |
| PF |
| AP |
| QF |
| DP |
| PQ |
| AP |
| QF |
(ii)判断出DQ的中点的路径为△BDQ的中位线MN.求出QF、BF的长度,利用勾股定理求出BQ的长度,再根据中位线性质求出MN的长度,即所求之路径长.
解答:(1)证明:∵BD⊥BE,
∴∠1+∠2=180°-90°=90°,
∵∠C=90°,
∴∠2+∠E=180°-90°=90°,
∴∠1=∠E,
∵在△ABD和△CEB中,
,
∴△ABD≌△CEB(AAS),
∴AB=CE,
∴AC=AB+BC=AD+CE;
(2)(i)如图,过点Q作QF⊥BC于F,
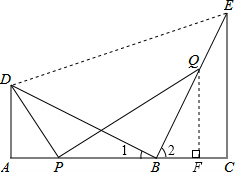
则△BFQ∽△BCE,
∴
=
,
即
=
,
∴QF=
BF,
∵DP⊥PQ,
∴∠ADP+∠FPQ=180°-90°=90°,
∵∠FPQ+∠PQF=180°-90°=90°,
∴∠ADP=∠FPQ,
又∵∠A=∠PFQ=90°,
∴△ADP∽△FPQ,
∴
=
,
即
=
,
∴5AP-AP2+AP•BF=3•
BF,
整理得,(AP-BF)(AP-5)=0,
∵点P与A,B两点不重合,
∴AP≠5,
∴AP=BF,
由△ADP∽△FPQ得,
=
,
∴
=
;
(ii)线段DQ的中点所经过的路径(线段)就是△BDQ的中位线MN.
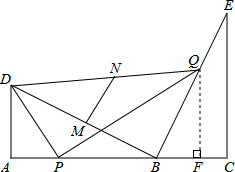
由(2)(i)可知,QF=
AP.
当点P运动至AC中点时,AP=4,∴QF=
.
∴BF=QF×
=4.
在Rt△BFQ中,根据勾股定理得:BQ=
=
=
.
∴MN=
BQ=
.
∴线段DQ的中点所经过的路径(线段)长为
.
∴∠1+∠2=180°-90°=90°,
∵∠C=90°,
∴∠2+∠E=180°-90°=90°,
∴∠1=∠E,
∵在△ABD和△CEB中,
|
∴△ABD≌△CEB(AAS),
∴AB=CE,
∴AC=AB+BC=AD+CE;
(2)(i)如图,过点Q作QF⊥BC于F,

则△BFQ∽△BCE,
∴
| BF |
| BC |
| QF |
| CE |
即
| BF |
| 3 |
| QF |
| 5 |
∴QF=
| 5 |
| 3 |
∵DP⊥PQ,
∴∠ADP+∠FPQ=180°-90°=90°,
∵∠FPQ+∠PQF=180°-90°=90°,
∴∠ADP=∠FPQ,
又∵∠A=∠PFQ=90°,
∴△ADP∽△FPQ,
∴
| AD |
| PF |
| AP |
| QF |
即
| 3 |
| 5-AP+BF |
| AP |
| QF |
∴5AP-AP2+AP•BF=3•
| 5 |
| 3 |
整理得,(AP-BF)(AP-5)=0,
∵点P与A,B两点不重合,
∴AP≠5,
∴AP=BF,
由△ADP∽△FPQ得,
| DP |
| PQ |
| AP |
| QF |
∴
| DP |
| PQ |
| 3 |
| 5 |
(ii)线段DQ的中点所经过的路径(线段)就是△BDQ的中位线MN.

由(2)(i)可知,QF=
| 5 |
| 3 |
当点P运动至AC中点时,AP=4,∴QF=
| 20 |
| 3 |
∴BF=QF×
| 3 |
| 5 |
在Rt△BFQ中,根据勾股定理得:BQ=
| BF2+QF2 |
42+(
|
| 4 |
| 3 |
| 34 |
∴MN=
| 1 |
| 2 |
| 2 |
| 3 |
| 34 |
∴线段DQ的中点所经过的路径(线段)长为
| 2 |
| 3 |
| 34 |
点评:本题考查了相似三角形的判定与性质,全等三角形的判定与性质,(1)求出三角形全等的条件∠1=∠E是解题的关键,(2)(i)根据两次三角形相似求出AP=BF是解题的关键,(ii)判断出路径为三角形的中位线是解题的关键.

练习册系列答案
相关题目
 (2013•成都)如图,在△ABC中,∠B=∠C,AB=5,则AC的长为( )
(2013•成都)如图,在△ABC中,∠B=∠C,AB=5,则AC的长为( ) (2013•成都)如图,某山坡的坡面AB=200米,坡角∠BAC=30°,则该山坡的高BC的长为
(2013•成都)如图,某山坡的坡面AB=200米,坡角∠BAC=30°,则该山坡的高BC的长为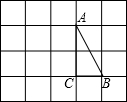 (2013•成都)如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°
(2013•成都)如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90° (2013•成都)如图,A,B,C为⊙O上相邻的三个n等分点,
(2013•成都)如图,A,B,C为⊙O上相邻的三个n等分点,