题目内容
 (2013•成都)如图,A,B,C为⊙O上相邻的三个n等分点,
(2013•成都)如图,A,B,C为⊙O上相邻的三个n等分点, |
| AB |
 |
| BC |
 |
| BC |
c+
b
| 2 |
c+
b
;当n=12时,p=| 2 |
c+
b
| ||||
| 2 |
c+
b
.
| ||||
| 2 |
(参考数据:sin15°=cos75°=
| ||||
| 4 |
| ||||
| 4 |
分析:如解答图所示,作辅助线,构造相似三角形.首先,在AE上取一点D,使ED=EC,连接CD,则△ABC与△CED为顶角相等的两个等腰三角形,所以△ABC∽△CED,得到
=
;其次,证明△ACD∽△BCE,得到
=
;由EA=ED+DA,整理得到p的通项公式为:p=c+2cos
•b.将n=4,n=12代入,即可求得答案.
| AC |
| BC |
| CD |
| EC |
| DA |
| EB |
| AC |
| BC |
| 180 |
| n |
解答: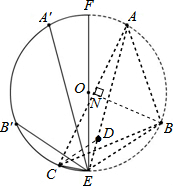 解:如解答图所示,连接AB、AC、BC.
解:如解答图所示,连接AB、AC、BC.
由题意,点A、B、C为圆上的n等分点,
∴AB=BC,∠ACB=
×
=
(度).
在等腰△ABC中,过顶点B作BN⊥AC于点N,
则AC=2CN=2BC•cos∠ACB=2cos
•BC,
∴
=2cos
.
连接AE、BE,在AE上取一点D,使ED=EC,连接CD.
∵∠ABC=∠CED,
∴△ABC与△CED为顶角相等的两个等腰三角形,
∴△ABC∽△CED.
∴
=
,∠ACB=∠DCE.
∵∠ACB=∠ACD+∠BCD,∠DCE=∠BCE+∠BCD,
∴∠ACD=∠BCE.
在△ACD与△BCE中,
∵
=
,∠ACD=∠BCE,
∴△ACD∽△BCE.
∴
=
,
∴DA=
•EB=2cos
•EB.
∴EA=ED+DA=EC+2cos
•EB.
由折叠性质可知,p=EA′=EA,b=EB′=EB,c=EC.
∴p=c+2cos
•b.
当n=4时,p=c+2cos45°•b=c+
b;
当n=12时,p=c+2cos15°•b=c+
b.
故答案为:c+
b,c+
b.
 解:如解答图所示,连接AB、AC、BC.
解:如解答图所示,连接AB、AC、BC.由题意,点A、B、C为圆上的n等分点,
∴AB=BC,∠ACB=
| 1 |
| 2 |
| 360 |
| n |
| 180 |
| n |
在等腰△ABC中,过顶点B作BN⊥AC于点N,
则AC=2CN=2BC•cos∠ACB=2cos
| 180 |
| n |
∴
| AC |
| BC |
| 180 |
| n |
连接AE、BE,在AE上取一点D,使ED=EC,连接CD.
∵∠ABC=∠CED,
∴△ABC与△CED为顶角相等的两个等腰三角形,
∴△ABC∽△CED.
∴
| AC |
| BC |
| CD |
| EC |
∵∠ACB=∠ACD+∠BCD,∠DCE=∠BCE+∠BCD,
∴∠ACD=∠BCE.
在△ACD与△BCE中,
∵
| AC |
| BC |
| CD |
| EC |
∴△ACD∽△BCE.
∴
| DA |
| EB |
| AC |
| BC |
∴DA=
| AC |
| BC |
| 180 |
| n |
∴EA=ED+DA=EC+2cos
| 180 |
| n |
由折叠性质可知,p=EA′=EA,b=EB′=EB,c=EC.
∴p=c+2cos
| 180 |
| n |
当n=4时,p=c+2cos45°•b=c+
| 2 |
当n=12时,p=c+2cos15°•b=c+
| ||||
| 2 |
故答案为:c+
| 2 |
| ||||
| 2 |
点评:本题是几何综合题,难度很大.解决本题,需要综合运用圆、相似三角形、等腰三角形、三角函数、折叠性质等多个知识点,对几何综合能力要求很高.本题解答过程中,求得p的通项公式:p=c+2cos
•b,这样的结果更具普遍性;也可以按照题中要求,对于4等分或12等分的情况分别求解.
| 180 |
| n |

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 (2013•成都)如图,在△ABC中,∠B=∠C,AB=5,则AC的长为( )
(2013•成都)如图,在△ABC中,∠B=∠C,AB=5,则AC的长为( ) (2013•成都)如图,某山坡的坡面AB=200米,坡角∠BAC=30°,则该山坡的高BC的长为
(2013•成都)如图,某山坡的坡面AB=200米,坡角∠BAC=30°,则该山坡的高BC的长为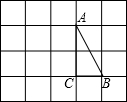 (2013•成都)如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°
(2013•成都)如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90° (2013•成都)如图,点B在线段AC上,点D,E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
(2013•成都)如图,点B在线段AC上,点D,E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.